1) . Докажем справедливость неравенства для всех таких переменных. Заметим, что , последнее неравенство получилось следующим образом: возведем обе части неравенства в квадрат и вычтем единицу, получим: , последняя величина больше , поэтому больше 1.
2) . Тогда нужно доказать . Но .
Объединив эти случаи, приходим к неравенству , верному для любого . Итого: , значит исходное неравенство не выполнено ни при каком
Заметим, что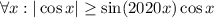 . Теперь рассмотрим два случая:
. Теперь рассмотрим два случая:
1) . Докажем справедливость неравенства
. Докажем справедливость неравенства 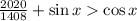 для всех таких переменных. Заметим, что
для всех таких переменных. Заметим, что 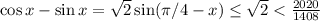 , последнее неравенство получилось следующим образом: возведем обе части неравенства в квадрат и вычтем единицу, получим:
, последнее неравенство получилось следующим образом: возведем обе части неравенства в квадрат и вычтем единицу, получим: 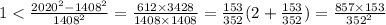 , последняя величина больше
, последняя величина больше 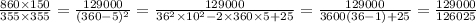 , поэтому больше 1.
, поэтому больше 1.
2)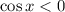 . Тогда нужно доказать
. Тогда нужно доказать 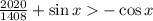 . Но
. Но 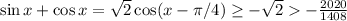 .
.
Объединив эти случаи, приходим к неравенству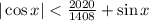 , верному для любого
, верному для любого  . Итого:
. Итого: 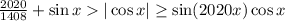 , значит исходное неравенство не выполнено ни при каком
, значит исходное неравенство не выполнено ни при каком