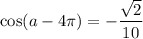5. Вычислите cos (а — 4π), если tg²a = 49 и
π/2<а<π

Во-первых, в силу периодичности искомое выражений можно упростить:

Так как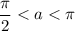 , то рассматриваемый угол принадлежит второй четверти, где косинус отрицательный.

Запишем формулу:

Выражаем косинус, учитывая его знак:

Подставляем значение квадрата тангенса:

ответ: