x² -x (√7 - 2 ) -2√7 = 0
а что непонятного ?
я же написал, что дискриминант для квадратного уравнения
ax^2 + bx + c = 0
D=b^2 - 4ac
еще никто не отменял
здесь такие a=1 b=-(√7-2) c=-2√7
D=(-(√7-2))² - 4 *1*(-2√7) = √7² - 4*√4 + 2² + 8√7 = √7 +2*2*√7 + 2² = (√7 + 2)²
√D = √7 + 2
x₁₂ = ((√7-2) +- (√7 + 2))/2 = -2 √7
ответ {-2, √7}
- можно открыть скобки и получить уравнение
x² -x √7 + 2 x -2√7 = 0
x(x -√7) + 2 (x -√7) = 0
(x + 2)(x - √7) = 0
- можно через теорему Виета
x1 + x2= -b/a = √7 - 2
x1*x2 = -2√7
и везде получаются одни и те же корни
что сложного ??? если решений много
5) x=0, x= -2,5
6) f(1)=5
7) 500500
Объяснение:
5)
x ≠ -1, x ≠ -2, x ≠ -3, x ≠ -4
5x³+25x²+30x+8x²+40x+48=5x³+25x²+20x+12x²+60x+48
4x²+10x=0 ⇒ x=0, x= -2,5
6)
x+1=2x-1 ⇒ x= 2
7) 1000·999-998·997+996·995-994·993-...+4·3-2·1
1000·999-998·997=(2+998)·999-998·997=2·999+998·999-998·997=
=2·999+2·998=2·(999+998)
996·995-994·993=(2+994)·995-994·993=2·995+994·995-994·993=
=2·995+2·994=2·(995+994)
...
4·3-2·1=(2+2)·3-2·1=2·3+2·3-2·1=2·3+2·2=2·(3+2)
1000·999-998·997+996·995-994·993-...+4·3-2·1= =2·(999+998)+2·(995+994)+...+2·3+2·2=
=2·(999+995+991+...+3)+2·(998+994+990+...+2)=
=2·(3+999):2·((999-3):4+1)+2·(2+998):2·((998-2):4+1)=
=1002·250+1000·250=250·2002=500500
x² -x (√7 - 2 ) -2√7 = 0
а что непонятного ?
я же написал, что дискриминант для квадратного уравнения
ax^2 + bx + c = 0
D=b^2 - 4ac
еще никто не отменял
здесь такие a=1 b=-(√7-2) c=-2√7
D=(-(√7-2))² - 4 *1*(-2√7) = √7² - 4*√4 + 2² + 8√7 = √7 +2*2*√7 + 2² = (√7 + 2)²
√D = √7 + 2
x₁₂ = ((√7-2) +- (√7 + 2))/2 = -2 √7
ответ {-2, √7}
- можно открыть скобки и получить уравнение
x² -x √7 + 2 x -2√7 = 0
x(x -√7) + 2 (x -√7) = 0
(x + 2)(x - √7) = 0
- можно через теорему Виета
x1 + x2= -b/a = √7 - 2
x1*x2 = -2√7
и везде получаются одни и те же корни
что сложного ??? если решений много
5) x=0, x= -2,5
6) f(1)=5
7) 500500
Объяснение:
5)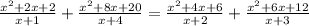
x ≠ -1, x ≠ -2, x ≠ -3, x ≠ -4
5x³+25x²+30x+8x²+40x+48=5x³+25x²+20x+12x²+60x+48
4x²+10x=0 ⇒ x=0, x= -2,5
6)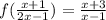
x+1=2x-1 ⇒ x= 2
7) 1000·999-998·997+996·995-994·993-...+4·3-2·1
1000·999-998·997=(2+998)·999-998·997=2·999+998·999-998·997=
=2·999+2·998=2·(999+998)
996·995-994·993=(2+994)·995-994·993=2·995+994·995-994·993=
=2·995+2·994=2·(995+994)
...
4·3-2·1=(2+2)·3-2·1=2·3+2·3-2·1=2·3+2·2=2·(3+2)
1000·999-998·997+996·995-994·993-...+4·3-2·1= =2·(999+998)+2·(995+994)+...+2·3+2·2=
=2·(999+995+991+...+3)+2·(998+994+990+...+2)=
=2·(3+999):2·((999-3):4+1)+2·(2+998):2·((998-2):4+1)=
=1002·250+1000·250=250·2002=500500