ответ:
ОДЗ:
Замена:
По методу интервалов выясняем знаки неравенства и получаем:
Обратная замена:
Объединяем все три условия и получаем:
ответ:![x \in [1; \ 5]](/tpl/images/0205/7464/e62de.png)
ОДЗ: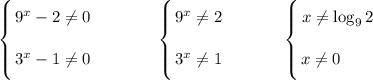
Замена: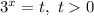
ОДЗ: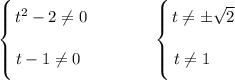
По методу интервалов выясняем знаки неравенства и получаем:
Обратная замена:
Объединяем все три условия и получаем:
ответ:![x \in \bigg[\log_{3}\dfrac{1}{2}; \ 0 \bigg) \cup (\log_{3}\sqrt{2}; \ 1]](/tpl/images/0205/7464/ef558.png)