n.s =4*2+3*(-1)+1*(-5) =0 ⇒ n ⊥ s , т.е. прямая параллельно плоскости или лежит на ней, но точка m₀(1; -3; -2) не лежит на плоскости, действительно 4*1+3*(-3)++1*(-5)+3 ≠0 (не удовл. уравн. ),значит прямая не лежит на плоскости. нажми выше, чтобы получить доступ. 4.2. 5 оценок. 5 оценок. достаточно было показать ,что точка m₀(1; -3; -2) ,через которой проходит данная линия не лежит на плоскости 4x+3y+z+3=0 т.е. 4*1+3*(-3)+1*(-2)+3 = -4 ≠0.
ответ:
n.s =4*2+3*(-1)+1*(-5) =0 ⇒ n ⊥ s , т.е. прямая параллельно плоскости или лежит на ней, но точка m₀(1; -3; -2) не лежит на плоскости, действительно 4*1+3*(-3)++1*(-5)+3 ≠0 (не удовл. уравн. ),значит прямая не лежит на плоскости. нажми выше, чтобы получить доступ. 4.2. 5 оценок. 5 оценок. достаточно было показать ,что точка m₀(1; -3; -2) ,через которой проходит данная линия не лежит на плоскости 4x+3y+z+3=0 т.е. 4*1+3*(-3)+1*(-2)+3 = -4 ≠0.
объяснение:
ну вроде так если неправильно сори брат
104.
a) cos 120 =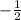
б) sin(-150)= -sin 150=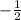
в) tg(-225)= -tg 225 = -1
г) cos(-225)=cos 225=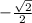
д) cos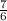
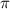= cos 630 = 0
е)sin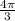
= sin 240 =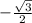
106.
а) sin (
-
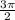) = sin (
-270) = sin (270-
) = -cos 
б) cos (
-
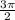)= cos (
-270) = cos (270-
) = -sin 
в) tg (
-2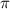
) = tg (
-360) = tg (360-
) = -tg 
Объяснение:
104.
cos(-α)= cos α
sin(-α)= -sin α
tg(-α)= -tg α
ctg(-α)= -ctg α
a) cos 120 =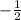
б) sin(-150)= -sin 150=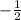
( т.к. sin непарная функция => sin(-α)= -sin α )
в) tg(-225)= -tg 225 = -1 ( т.к. tg непарная функция => tg(-α)= -tg α )
г) cos(-225)=cos 225=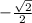
( т.к. cos парная функция => cos(-α)= cos α )
д) cos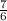
= 
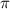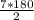=630, 630=360+270 ( 360 это один полный оборот)
=> cos 270 cos 270 = 0
е)sin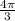
= sin 240 =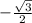
106.
В этом номере я использовал формулы приведения
их можно найти в интернете
а) sin (
-
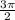) = sin (
-270) = sin (270-
) = -cos 
б) cos (
-
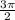)= cos (
-270) = cos (270-
) = -sin 
в) tg (
-2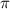
) = tg (
-360) = tg (360-
) = -tg 