6.Из класса где учатся 24 учащихся сколькими можно выбрать 2-х человек для дежурства?

Показать ответ

Ответ:

Говницооо

05.05.2021 00:03

Объяснение:

a) нет (любое отрицательное целое число не является натуральным, например -1)

б) да

в)нет ( например число 1,25)

г)Нет (например число √7 будет действительным и иррациональным)

3)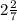 $2\frac{2}{7}$ = 16/7 = 160/70

2,2 = 22/10 = 144/70, значит 16/7>2,2

2,3 = 23/10 = 161/70, значит 16/7<2,3 , а значит правильный ответ 2 ( не знаю почему учитель поставил -, наверное ошибся)

ответ: 2

4) Площадь прямоугольника находится по формул S = a*b, где a и b его стороны

$S=(5-\sqrt{3})*(5+\sqrt{3} )$ тут мы видим разность квадратов

S = 5²-√3² = 25 -3 = 22

ответ : 22

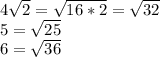
5) $4\sqrt{2} = \sqrt{16*2} = \sqrt{32} \\5 = \sqrt{25} \\6 = \sqrt{36}$

$\sqrt{25}$ , значит 4√2 находится между ними

середина между 25 и 36 - число 31, а т.к 32>31, то точка будет ближе к числу 6, а значит ответ 3)P

ответ: 3

$x = 6, \sqrt{3 - 2*6} = \sqrt{-9} \\x = 0, \sqrt{3 - 2 *0} =\sqrt{3} \\x = -2, \sqrt{3-2*(-2)} =\sqrt{3+4} = \sqrt{7} \\x = -3, \sqrt{3 - 2 *(-3)} =\sqrt{3+6} = \sqrt{9} = 3$

В 1 случае нет решения, т.к корень отрицательный

Во 2 и 3 корни иррациональные

В 4 уравнение мы получили число 3 - рациональное, значит ответ 4

ответ: 4

$x^{2} -4x -3 = 0$

D= (-4)²-4*1*(-3) = 16 + 12 =28

$x(1) = \frac{4+\sqrt{28} }{2} = \frac{4+2\sqrt{7} }{2} = \frac{2(2+\sqrt{7}) }{2} = 2+\sqrt{7}$

$x(2) = \frac{4-\sqrt{28} }{2} = \frac{4-2\sqrt{7} }{2} = \frac{2(2-\sqrt{7}) }{2} = 2-\sqrt{7}$ - подходит

б)5x²-x = 0

x(5x-1)=0

x = 0 или 5x -1 = 0

5x = 1

x = 0,2 - не подходит, т.к тут корни уравнения рациональные

в) 1 - 4x²= 0

4x² = 1

$x^{2} =\frac{1}{4}\\x = \sqrt{\frac{1}{4} } \\x(1) = -\frac{1}{2} \\x(2) =\frac{1}{2}$ - не подходит, т.к тут рациональные корни уравнения

ответ: 1

8) тут просто подставляем x и y

M: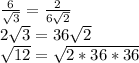 $\frac{6}{\sqrt{3} } = \frac{2}{6\sqrt{2} } \\2\sqrt{3} = 36\sqrt{2} \\\sqrt{12} =\sqrt{2*36*36}$ - неверно

N: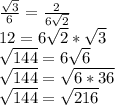 $\frac{\sqrt{3} }{6} =\frac{2}{6\sqrt{2} } \\12 = 6\sqrt{2} *\sqrt{3} \\\sqrt{144}= 6\sqrt{6}\\\sqrt{144} = \sqrt{6*36} \\\sqrt{144}=\sqrt{216}$ - неверно

P: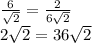 $\frac{6}{\sqrt{2} } =\frac{2}{6\sqrt{2} } \\2\sqrt{2} = 36\sqrt{2}$ - неверно

ну методом исключения правильный ответ 4) Q , но лучше перепроверить

Q: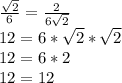 $\frac{\sqrt{2} }{6} =\frac{2}{6\sqrt{2} } \\12 = 6*\sqrt{2} *\sqrt{2} \\12 = 6 *2\\12 = 12$ - истина

ответ: 4

0,0(0 оценок)

Ответ:

зарина298

21.09.2020 22:53

Y = 5*x-sin(2*x)
1. Находим интервалы возрастания и убывания.
Первая производная равна:.
f'(x) = -2cos(2x)+5
Находим нули функции. Для этого приравниваем производную к нулю
-2cos(2x)+5 = 0
Для данного уравнения корней нет.
2. Находим интервалы выпуклости и вогнутости функции.
Вторая производная равна:
f''(x) = 4sin(2x)
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
4sin(2x) = 0
Откуда точки перегиба:
x1 = 0
На интервале (-∞ ;0) f''(x) < 0, функция выпукла
На интервале (0; +∞) f''(x) > 0, функция вогнута

0,0(0 оценок)

Популярные вопросы: Алгебра