Алгебра: 6. Обчисліть значення виразу , якщо a = -4.А) -40; Б) 40; В) 100; Г) -100.

1)Введём замену: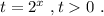 По теореме Виета:.Но так как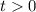 , то -2 не является решением этого уравнения. Выполняем обратную замену:ответ: 4.2)ответ: -2.3)Введём замену: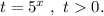 По теореме Виета:Но так как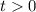 , то -1 не является решением этого уравнения. Выполняем обратную замену:ответ: 1.4)ответ: 1.5)Для начала кое-что учтём: подкоренное выражение всегда неотрицательно. То есть:Продолжаем решение:Введём замену: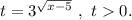 По теореме Виета:Но так как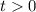 , то -3 не является решением этого уравнения. Выполняем обратную замену:ответ: 9....

6. Обчисліть значення виразу ${2.5a}^{2}$
, якщо a = -4.
А) -40; Б) 40; В) 100; Г) -100.

Показать ответ

Ответ:

akikoaki

13.08.2022 23:46

$4^x - 14\cdot 2^x - 32 = 0\\\\(2^2)^x - 14\cdot 2^x - 32 = 0\\\\(2^x)^2 - 14\cdot 2^x - 32 = 0$

Введём замену: $t = 2^x\ , t0\ .$

t^2 - 14t - 32 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}t_{1}t_{2} = -32\\t_{1} + t_{2} = 14\end{cases}\end{equation*}\ \ \ \ \ \Big|\ \boxed{t = 16; t = -2}$ .

Но так как t 0 , то -2 не является решением этого уравнения. Выполняем обратную замену:

$2^x = 16\\2^x = 2^4\\\\\boxed{\textbf{x = 4}}$

ответ: 4.

$4^{x-3} = 32^x\\\\(2^2)^{x-3} = (2^5)^x\\\\2^{2(x-3)} = 2^{5x}\\\\2(x-3) = 5x\\\\2x - 6 - 5x = 0\\\\-3x = 6\\\\\boxed{\textbf{x = -2}}$

ответ: -2.

$5^{2x} - 4\cdot 5^x - 5 = 0\\\\(5^x)^2 - 4\cdot 5^x - 5 = 0$

Введём замену: $t = 5^x\ ,\ t 0.$

t^2 - 4t - 5 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}t_{1}t_{2} = -5\\t_{1}+t_{2} = 4\end{cases}\end{equation*}\ \ \ \ \ \Big|\ \boxed{t = 5; t = -1}$

Но так как t 0 , то -1 не является решением этого уравнения. Выполняем обратную замену:

$5^x = 5\\\\\boxed{\textbf{x = 1}}$

ответ: 1.

$5^{x+2} + 11\cdot 5^x = 180\\\\5^x \cdot 5^2 + 11\cdot 5^x = 180\\\\5^x(25+11) = 180\\\\5^x\cdot 36 = 180\ \ \ \Big| :36\\\\5^x = 5\\\\\boxed{\textbf{x = 1}}$

ответ: 1.

$9^{\sqrt{x-5}} - 27 = 6\cdot 3^{\sqrt{x-5}}$

Для начала кое-что учтём: подкоренное выражение всегда неотрицательно. То есть:

$x - 5 \geq 0\\x \geq 5$

Продолжаем решение:

$(3^2)^{\sqrt{x-5}} - 6\cdot 3^{\sqrt{x-5}} - 27 = 0\\\\(3^{\sqrt{x-5}})^2 - 6\cdot 3^{\sqrt{x-5}} - 27 = 0$

Введём замену: $t = 3^{\sqrt{x-5}}\ ,\ t0.$

t^2 - 6t - 27 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}t_{1}t_{2} = -27\\t_{1}+t_{2} = 6\end{cases}\end{equation*}\ \ \ \ \ \Big|\ \boxed{t = 9; t = -3}$

Но так как t 0 , то -3 не является решением этого уравнения. Выполняем обратную замену:

$3^{\sqrt{x-5}} = 9\\\\3^{\sqrt{x-5}} = 3^2\\\\\sqrt{x-5} = 2\\\\x - 5 = 4\\\\\boxed{\textbf{x = 9}}$

ответ: 9.

0,0(0 оценок)

Ответ:

Albina1967

26.09.2020 10:33

X^2+4x = 4 + 2|x+2|

прибавим 4 к обеим частям уравнения
x^2+4x + 4 = 8 + 2|x+2|

левая часть - это разложенный по формуле квадрат суммы x+2
(x+2)^2 = 8+2|x+2|

Вычтем из обеих частей 8 и затем поделим на 2
((x+2)^2 - 8)/2 = |x+2|

((x+2)^2)/ 2 - 4 = |x+2|

Сделаем замену: x+2 = t. Тогда уравнение примет вид
t^2/2-4 = |t|

Избавимся от модуля - возведем обе части в квадрат
(t^2/2-4)^2 = t^2

Разложим левую часть по формуле квадрата разности. Получим биквадратное уравнение
t^4/4 - 4t^2+16 = t^2

Сделаем замену t^2 = z. Тогда уравнение примет вид
z^2/4 - 4z +16 = z
или
z^2/4 - 5z +16 = 0

Найдем дискриминант:
D = (-5)^2 - 4*1/4*16 = 25-16 = 9
D>0, значит два корня
z1 = (5+3)*2= 16
z2 = (5-3)*2 = 4

Делаем обратные замены

z1 = t1^2 = 16 >>> t1 = +/- 4. Обозначим t11 = 4, t12 = -4
z2 = t2^2 = 4 >>>t2 = +/- 2. Обозначим t21 = 2, t22 = -2

Снова делаем обратные замены

t11 = x11+2 = 4 >>> x11 = 2
t12=x12+2 = -4 >>>x12 = -6
t21=x21+2 = 2 >>>x21 = 0
t22=x22+2= -2 >>>x22 = -4

0,0(0 оценок)

Популярные вопросы: Алгебра