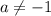Заметим, что множество значений правой части уравнения вне зависимости от параметров и будет от -2 до 0.
Когда равенство выполняется при всех , графики левой и правой частей совпадают, то есть множество значений левой части уравнения тоже должно быть от -2 до 0.
Множество значений будет ограничиваться отрезком .
Множество значений будет ограничиваться отрезком .
Множество значений будет ограничиваться отрезком .
Тогда должна выполняться система:
Проверим, являются ли полученные значения ответом:
Равенство верно для всех , поэтому и являются ответом.
(см. объяснение)
Объяснение:
Заметим, что множество значений правой части уравнения вне зависимости от параметров и
и 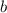 будет от -2 до 0.
будет от -2 до 0.
Когда равенство выполняется при всех , графики левой и правой частей совпадают, то есть множество значений левой части уравнения тоже должно быть от -2 до 0.
, графики левой и правой частей совпадают, то есть множество значений левой части уравнения тоже должно быть от -2 до 0.
Множество значений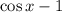 будет ограничиваться отрезком
будет ограничиваться отрезком ![[-2;\; 0]](/tpl/images/4513/6771/c3b39.png) .
.
Множество значений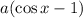 будет ограничиваться отрезком
будет ограничиваться отрезком ![[-2a;\;0]](/tpl/images/4513/6771/09a95.png) .
.
Множество значений будет ограничиваться отрезком
будет ограничиваться отрезком ![[-2a+b^2;\;b^2]](/tpl/images/4513/6771/71911.png) .
.
Тогда должна выполняться система:
Проверим, являются ли полученные значения ответом:
Равенство верно для всех , поэтому
, поэтому 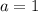 и
и 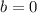 являются ответом.
являются ответом.
Задание выполнено!
(0;0); (1;0)
Объяснение:
Равенство выполнено для всех значений переменной, значит, оно верно и для x=0:
Левая часть полученного уравнения не меньше 1, правая - не больше 1. Значит, уравнение равносильно системе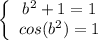
Из 1ого уравнения получим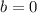 , которое удовлетворяет и 2ому уравнению системы.
, которое удовлетворяет и 2ому уравнению системы.
Подставив в условие, получим:
1)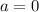
После подстановки получим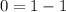 - верно
- верно
2)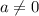
Равенство выполнено для всех значений переменной, значит, оно верно и для :
:
Равенство выполнено для всех значений переменной, значит, оно верно и для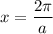 :
:
Но тогда, с учетом полученного выше условия, а может принимать значения 1 или -1:
2.1) - верно
- верно
2.2)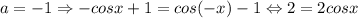 - очевидно, равенство не тождественное. Значит,
- очевидно, равенство не тождественное. Значит,