Две бригады, работая вместе выполняют некоторую работу за 2 дня. За сколько дней эту работу выполнила бы каждая бригада в отдельности, если первой бригаде на это нужно на 3 дня больше, чем второй?
Решение.
Пусть за дней всю работу выполнила бы первая бригада, тогда
за дней всю эту работу выполнила бы вторая бригада.
Примем весь объём работы за 1 (единицу), тогда
- производительность первой бригады;
- производительность первой бригады.
- общая производительность двух бригад.
Уравнение:
(
не удовлетворяет условию, т.к.
удовлетворяет условию.
За 6 дней всю работу выполнила бы первая бригада.
За 6-3=3 дня всю эту работу выполнила бы вторая бригада.
Две бригады, работая вместе выполняют некоторую работу за 2 дня. За сколько дней эту работу выполнила бы каждая бригада в отдельности, если первой бригаде на это нужно на 3 дня больше, чем второй?
Решение.
Пусть за дней всю работу выполнила бы первая бригада, тогда
дней всю работу выполнила бы первая бригада, тогда
за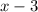 дней всю эту работу выполнила бы вторая бригада.
дней всю эту работу выполнила бы вторая бригада.
Примем весь объём работы за 1 (единицу), тогда
Уравнение:
За 6 дней всю работу выполнила бы первая бригада.
За 6-3=3 дня всю эту работу выполнила бы вторая бригада.
ответ: 6 дней; 3 дня.
Объяснение:
Пусть N=20. ⇒
В качестве случайной величины Х выступает количество холодильников, которые могут сломаться, равно 3.
Возможные значения, которые примет случайная величина Х: 1, 2, 3.
Обозначим соответствие А₁ - состояние 1-го холодильника; А₂ - состояние 2-го холодильника; состояние 3-го холодильника. ⇒
р(А₁)=р(А₂)=р(А₃)=0,3.
Вероятность того, что холодильник не сломается (противоположное событие) равно:
Для составления закона распределения рассчитываем следующие вероятности:
x | 1 | 2 | 3 |
----------------------------
p | 0,3 | 0,21 | 0,49 |
Вычислим математическое ожидание случайной величины:
Вычислим дисперсию случайной величины:
Вычислим среднеквадратическое отклонение случайной величины:
ответ: M(X)=2,19, σ(X)=0,868.