Алгебра: 732*569+288*560 49*780-78*390

732569+288560

49780-78390

Показать ответ

Ответ:

dashakoshelevap06xlg

01.02.2022 16:31

Пусть х(грн) - стоит 1кг апельсинов, а у(грн) - стоит 1кг лимонов, тогда 5кг апельсинов стоят 5х(грн), а 6кг лимонов стоят 6у(грн), вместе они стоят 150грн, получаем уравнение 5х+6у=150. 4кг апельсинов стоят 4х(грн), а 3кг лимонов 3у(грн), раз 4кг апельсинов дороже на 3грн, то получим уравнение 4х-3у=3. Составим и решим систему уравнений:5х+6у=150,4х-3у=3;Решим систему сложения, умножив второе уравнение на 2, получим:5х+6у=150,8х-6у=6; 13х=156,4х-3у=3; х=12,48-3у=3; х=12,-3у=-45; х=12,у=15.12(грн)-стоит 1кг апельсинов15(грн)-стоит 1кг лимонов

0,0(0 оценок)

Ответ:

ilia9999999999

26.02.2021 05:18

$\dfrac{a^4}{24} +\dfrac{a^3}{4} +\dfrac{11a^2}{24} +\dfrac{a}{4},\ a\in\mathbb{Z}$

Преобразуем выражение:

$\dfrac{a^4}{24} +\dfrac{a^3}{4} +\dfrac{11a^2}{24} +\dfrac{a}{4} =\dfrac{a^4}{24} +\dfrac{6a^3}{24} +\dfrac{11a^2}{24} +\dfrac{6a}{24} =\dfrac{a^4+6a^3+11a^2+6a}{24}$

Рассмотрим и преобразуем числитель:

a^4+6a^3+11a^2+6a=a(a^3+6a^2+11a+6)=

=a(a^3+a^2+5a^2+5a+6a+6)=a(a^2(a+1)+5a(a+1)+6(a+1))=

=a(a+1)(a^2+5a+6)=a(a+1)(a^2+2a+3a+6)=

=a(a+1)(a(a+2)+3(a+2))=a(a+1)(a+2)(a+3)

Получилось произведение четырех подряд идущих целых чисел.

Из четырех подряд идущих целых чисел гарантированно найдется хотя бы одно, кратное 3. Также, из четырех подряд идущих целых чисел найдется два четных числа, одно из которых не только четное, но и кратно 4.

Таким образом, в произведении гарантированно есть множители 3, 2 и 4. Тогда, такое произведение делится на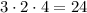 $3\cdot2\cdot4=24$ .