Перед нами система из уравнений, графиком каждого из которых является прямая. Применим геометрию и вспомним, что прямые могут пересекаться, совпадать или быть параллельными. В каждом из случаев будет одно решение, их бесконечное множество, отсутствие решений соответсвенно. Нас устраивает первый случай. Опишем его на языке математики, как , где - это угловой коэффициент (тангенс угла наклона).
Тогда выразим и из строк исходной системы.
При :
Решением будет пара чисел .
Значит такое значение параметра нам подходит.
При :
Тогда:
Итого получили, что при исходная система уравнений имеет ровно одно решение.
(см. объяснение)
Объяснение:
Перед нами система из уравнений, графиком каждого из которых является прямая. Применим геометрию и вспомним, что прямые могут пересекаться, совпадать или быть параллельными. В каждом из случаев будет одно решение, их бесконечное множество, отсутствие решений соответсвенно. Нас устраивает первый случай. Опишем его на языке математики, как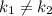
, где 
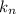- это угловой коэффициент (тангенс угла наклона).
Тогда выразим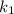
и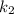 
из строк исходной системы.
При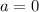
:
Решением будет пара чисел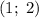
.
Значит такое значение параметра нам подходит.
При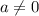
:
Тогда:
Итого получили, что при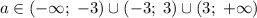
исходная система уравнений имеет ровно одно решение.
Задание выполнено!