Областью определения выражения являются все вещественные числа, кроме тех, при которых выражение не определено. В данном случае нет вещественных чисел, при которых выражение было бы неопределенным.
Запись в виде интервала:
(−∞,∞)
Нотация построения множества:
{x|x∈R}
Область значений - это набор всех допустимых значений y.Используйте график для определения области значений.
Запись в виде интервала:
(−∞,1]
Определяем область определения и область значений.
а) n-ый член геометрической прогрессии ищется по формуле:
Тогда пятый член этой прогрессии равен:
б) Аналогично по формуле n-го члена геом. прогрессии вычисляем девятый член прогрессии:
в) Сумма первых n членов геометрической прогрессии ищется по следующей формуле:
Тогда сумма первых восьми членов этой прогрессии равна:
г) Аналогично с в) по формуле суммы n первых членов геометрической прогрессии вычисляем сумму первых пяти членов этой прогрессии:
д) Предполагается, что нужно найти сумму бесконечно убывающей геометрической прогрессии:
Тогда
А) -36; - 12; -4;
Сумма бесконечно уб. г.п.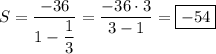
Б)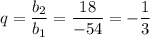
Сумма бесконечно убывающей геометрической прогрессии:
e) используя n-ый член геометрической прогрессии, рассмотрим пятый член этой прогрессии:
Так как по условию q>0, то q=3
Сумма первых восьми членов этой прогрессии равна:
Областью определения выражения являются все вещественные числа, кроме тех, при которых выражение не определено. В данном случае нет вещественных чисел, при которых выражение было бы неопределенным.
Запись в виде интервала:
(−∞,∞)
Нотация построения множества:
{x|x∈R}
Область значений - это набор всех допустимых значений y.Используйте график для определения области значений.
Запись в виде интервала:
(−∞,1]
Определяем область определения и область значений.
Область определения:
(−∞,∞),{x|∈R}
Область значений:
(−∞,1],{y|y≤1}
Объяснение: