Уравнение не имеет корней если дискриминант отрицательный или (а-6)²-16=а²-12*а+36-16=а²-12*а+20<0. Для второго уравнения D=144-80=64 и корни а1=(12+8)/2=10 и а2=(1248)/2=2. Так как у второго уравнения ветви параболы направлены вверх, то искомые значения а лежат в пределах от а21 до а2 (от 2 до 10).
Чтобы квадратное уравнение не имело действительных корней, его дискриминант должен быть меньше нуля.
Находим корни . По теореме Виета корни — 2 и 10. Ветви параболы направлены вверх, значит, нам нужен промежуток между корнями, т.к. там значение выражение отрицательно.
Уравнение не имеет корней если дискриминант отрицательный или (а-6)²-16=а²-12*а+36-16=а²-12*а+20<0. Для второго уравнения D=144-80=64 и корни а1=(12+8)/2=10 и а2=(1248)/2=2. Так как у второго уравнения ветви параболы направлены вверх, то искомые значения а лежат в пределах от а21 до а2 (от 2 до 10).
ответ: от 2 до 10
Чтобы квадратное уравнение не имело действительных корней, его дискриминант должен быть меньше нуля.
Находим корни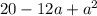 . По теореме Виета корни — 2 и 10. Ветви параболы направлены вверх, значит, нам нужен промежуток между корнями, т.к. там значение выражение отрицательно.
. По теореме Виета корни — 2 и 10. Ветви параболы направлены вверх, значит, нам нужен промежуток между корнями, т.к. там значение выражение отрицательно.
ответ: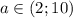 .
.