Теорема Виета гласит, что произведение корней приведенного квадратного уравнения равно свободному члену (q), а их сумма равна числу обратному второму коэффициенту (-p)
x₁ · x₂ = q
x₁ + x₂ = -p
Часто нам будут даваться не приведенные квадратные уравнение, а обычные, они имеют вид
ax² + bx + c = 0 (то же приведенное, но с коэффициентом перед x-ом)
что бы получить из обычного квадратного уравнение приведенное, нужно разделить его на a. От сюда сумма и произведение корней обычного квадратного уравнения равны:
Коли просите, не могу отказать ;) Я дам только решение, без доказательств и тонкостей, все это можно найти в интернете при должном желании.
x² + px + q = 0 - приведенное квадратное уравнение
Теорема Виета гласит, что произведение корней приведенного квадратного уравнения равно свободному члену (q), а их сумма равна числу обратному второму коэффициенту (-p)
x₁ · x₂ = q
x₁ + x₂ = -p
Часто нам будут даваться не приведенные квадратные уравнение, а обычные, они имеют вид
ax² + bx + c = 0 (то же приведенное, но с коэффициентом перед x-ом)
что бы получить из обычного квадратного уравнение приведенное, нужно разделить его на a. От сюда сумма и произведение корней обычного квадратного уравнения равны:
x₁ · x₂ =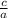
x₁ + x₂ = -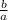
Пример:
x² - 4x + 3 = 0
Тогда корни:
x₁ = 1
x₂ = 3
Надеюсь, что все понятно)
В решении.
Объяснение:
Объяснение:
Найдите сумму и разность многочленов А и В. Запишите результат как многочлен стандартного вида.
1) Записать в одну строку, второй многочлен в скобках, между ними знак + или -.
2)Раскрыть скобки. Если между многочленами знак +, во втором многочлене знаки не меняются, если перед скобками знак -, меняются на противоположные.
3)Привести подобные члены.
4)Записать результат в стандартном виде, т.е., в порядке убывания степеней.
а) 5х² - 0,18у³ + (6,2х² + 7у³)=
=5х² - 0,18у³ + 6,2х² + 7у³=
=6,82у³ + 11,х²;
б) 5х² - 0,18у³ - (6,2х² + 7у³)=
=5х² - 0,18у³ - 6,2х² - 7у³=
= -7,18у³ - 1,2х².