Различают несколько частот, если речь об абсолютной частоте, то это целое число, которое показывает, сколько раз данное значение повторяется в выборке. Сумма абсолютных частот всегда равна объему выборки. В Вашем примере этот объем равен 50 /суммируем последний столбец частот./
Что касаемо относительной частоты, то она получается из абсолютной, если ее поделить на объем выборки, т.е. она будет дробным числом от 0 до 1 и указывает долю, которую данное значение составляет от всего объема выборки. Сумма относительных частот всегда равна 1. Я не сокращаю, прохожу по Вашему примеру.
2/50;3/50...10/50;2/50 В сумме единица.
Теперь накопленные относительные частоты, они указывают на долю элементов выборки, которые не превышает данного значения. Накопленные частоты получаются из относительных накопительным суммированием, и последняя накопленная частота всегда равна 1. По Вашему примеру,
ответ: Минимум (-3;-1). Рост функции на интервале (-3;+∞). Функция убывает на промежутке (-∞;-3)
Объяснение:
Наименьшее значение:
Перед нами уравнение параболы. Известно, что экстремальное значение параболы достигается при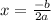
(здесь b - коэффициент при x, а а - коэффициент при x^2)
Находим x:
x = -3 ⇒ подставляем это значение в функцию ⇒ y = -1 (данный y - минимум, которого может достичь функция)
Точка минимума - (-3;-1)
Промежуток, на котором функция возрастает:
Понятно, что данная парабола ветвями вверх, так как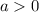
. Значит, функция возрастает после прохождения своего минимума:
Рост функции:
x ∈ (-3; +∞)
Промежуток на котором функция убывает:
Функция убывает пока не достигнет своего минимума
Уменьшение функции:
x ∈ (-∞; -3)
Различают несколько частот, если речь об абсолютной частоте, то это целое число, которое показывает, сколько раз данное значение повторяется в выборке. Сумма абсолютных частот всегда равна объему выборки. В Вашем примере этот объем равен 50 /суммируем последний столбец частот./
Что касаемо относительной частоты, то она получается из абсолютной, если ее поделить на объем выборки, т.е. она будет дробным числом от 0 до 1 и указывает долю, которую данное значение составляет от всего объема выборки. Сумма относительных частот всегда равна 1. Я не сокращаю, прохожу по Вашему примеру.
2/50;3/50...10/50;2/50 В сумме единица.
Теперь накопленные относительные частоты, они указывают на долю элементов выборки, которые не превышает данного значения. Накопленные частоты получаются из относительных накопительным суммированием, и последняя накопленная частота всегда равна 1. По Вашему примеру,
2/50
5/50
11/50
28/50
38/50
48/50
50/50
Надеюсь. все ясно?