Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Третье важное свойство задается теоремой: если функции заданы над областью целостности, то уравнение эквивалентно совокупности уравнений: Это означает, что все корни первого уравнения являются корнями одного из двух других уравнений и позволяет находить корни частями.
S полн. пов =2430
Объяснение:
Sполн. пов=Sбок.пов+2*Sосн
Sбок.пов=Росн*Н, Н - высота призмы
Sосн=S трапеции =(a+b)*h/2, h - высота трапеции
1. ABCD - трапеция
AB=25, BC=16, CD=17, AD=44.
дополнительные построения:
BM_|_AD, CN_|_AD, BC=MN=16
пусть DN=x, тогда
AD=AM+MN+ND
44=AM+16+x,
AM=44-(16+x), AM=28-x
2. рассмотрим прямоугольный треугольник АМВ:
∠M=90°
гипотенуза АВ=25
катет АМ=28-х
катет ВМ найти по теореме Пифагора:
AM²=AB²-BM²
AM²=25²-(28-x)²
AM²=-x²+56x-159
3. рассмотрим прямоугольный треугольник DNC:
гипотенуза CD=17
катет DN=x
катет CN найти по теореме Пифагора:
CN²=CD²-DN²
CN²=17²-x²
4. BM=CN, =>
уравнение: -х²+56x-159=17²-x²
56x=448
x=8
CN²=17²-8², CN=15
5.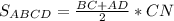
6. S полн. пов=(25+16+17+44)*15+2*450=2430