А1. Какое из чисел является корнем уравнения 3x2 = 5x + 12? 1) 1

2) 2

3) 3

4) 4

А2. Корнем какого уравнения является число -1?

1) x(x + 5)(x - 2) = 0

2) x(x + 5)(x - 2) = 12

3) х - 1 = 0

4) |x| = -1

А3. Выясните, какие из следующих уравнений равносильны:

A. х2 =25,

B. x - 5 = 0,

C. (x - 5)(x + 5) = 0.

1) В и С

2) А и В

3) А, В и С

4) А и С

В1. Сколько корней имеет уравнение |x| = 4?

С1. Составьте уравнение, корнем которого является число -7.

Для того, щоб подати дані вирази у вигляді стандартного многочлена, треба скористатися формулами скороченого множення:

а. (3-2х)(3+2х) + (2х-1)²  ⇒ (a-b)(a+b) +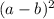 ⇒ 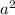- 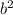+ a² - 2ab + b²;

(3-2х)(3+2х) + (2х-1)² =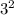 - 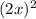+ (2x)² - 2×2x×1 + 1² = 9 - 4x² + 4x² - 4x +1 = 10 - 4x;

б. (3-4у)(3+4у)  ⇒ (a-b)(a+b);

(3-4у)(3+4у) =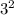 - 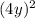= 9 - ;

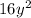в. (3-у)(9+3у+у²)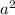  ⇒ (a-b)(+ab+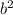) ⇒ a³- b³;

(3-у)(9+3у+у²)  = 3³- у³ = 27 - у³;

г. (2а-1)³ ⇒ (a-b)³ ⇒ a³ - 3a²b + 3ab² - b³;

(2а-1)³ = (2a)³ - 3×(2a)²×1 + 3×2a×1² - 1³ = 8a³ - 12a² + 6a - 1.

x−3∣≥1.8

x-3 \geq 1.8x−3≥1.8       или       x-3 \leq -1.8x−3≤−1.8

x \geq 1.8+3x≥1.8+3       или       x \leq -1.8+3x≤−1.8+3

x \geq 4.8x≥4.8            или       x \leq 1.2x≤1.2

[1.2][4.8]

xx  ∈ (-(−  ∞ ;1.2];1.2]  ∪ [4.8;+[4.8;+  ∞ ))

2)

|2-x|\ \textgreater \ \frac{1}{3}∣2−x∣ \textgreater 31

2-x\ \textgreater \ \frac{1}{3}2−x \textgreater 31         или       2-x\ \textless \ - \frac{1}{3}2−x \textless −31

-x\ \textgreater \ \frac{1}{3}-2−x \textgreater 31−2       или       -x\ \textless \ - \frac{1}{3} -2−x \textless −31−2

x\ \textless \ 1 \frac{2}{3}x \textless 132              или       x\ \textgreater \ 2 \frac{1}{3}x \textgreater 231

(1 2/3)(2 1/3)

xx  ∈ (-(−  ∞ ;1\frac{2}{3});132)  ∪ (2\frac{2}{3};+(232;+  ∞ ))

3)

| 3-x|\ \textless \ 1.2∣3−x∣ \textless 1.2

\left \{ {{3-x\ \textless \ 1.2} \atop {3-x\ \textgreater \ -1.2}} \right.{3−x \textgreater −1.23−x \textless 1.2

\left \{ {{-x\ \textless \ 1.2-3} \atop {-x\ \textgreater \ -1.2-3}} \right.{−x \textgreater −1.2−3−x \textless 1.2−3

\left \{ {{-x\ \textless \ -1.8} \atop {-x\ \textgreater \ -4.2}} \right.{−x \textgreater −4.2−x \textless −1.8

\left \{ {{x\ \textgreater \ 1.8} \atop {x\ \textless \ 4.2}} \right.{x \textless 4.2x \textgreater 1.8

(1.8)(4.2)

xx  ∈ (1.8;4.2)(1.8;4.2)

4)

|4+x | \leq 1.8∣4+x∣≤1.8

\left \{ {{4+x \leq 1.8} \atop { 4+x \geq -1.8}} \right.{4+x≥−1.84+x≤1.8