Для того, чтобы найти разность арифметической прогрессии, если известны первый и восьмой член прогрессии a1 = 4, а a18 = -11 вспомним формулу для нахождения n - го члена прогрессии.
Формула нахождения n - го члена арифметической прогрессии выглядит так:
an = a1 + (n - 1) * d;
Запишем формулу для нахождения 18 - го члена арифметической прогрессии.
Для того, чтобы найти разность арифметической прогрессии, если известны первый и восьмой член прогрессии a1 = 4, а a18 = -11 вспомним формулу для нахождения n - го члена прогрессии.
Формула нахождения n - го члена арифметической прогрессии выглядит так:
an = a1 + (n - 1) * d;
Запишем формулу для нахождения 18 - го члена арифметической прогрессии.
a18 = a1 + (18 - 1) * d = a1 + 17d;
Подставляем известные значения:
4 + 17d = -11;
Перенесем 4 в правую часть уравнения:
17d = -11 - 5;
17d = -15;
d = -15 : 17;
d = -15/17.
ответ: d = -15/17.
Объяснение:
1) Масштаб 1 : 2 000 000 означает, что
1 см = 2 000 000 см
1 см = 20 000 м
1 см = 20 км
2) Рассмотрим ΔАВС, в нем:
АВ = 5√3 см
АС = 5 см
∠АСВ = 120°
Пусть ВС = х, тогда, применяя теорему косинусов, получаем:
АВ² = АС² + ВС² - 2 · АВ · ВС · cos∠ACB
(5√3)² = 5² + x² - 2·5·x·cos120°
Знаем, что cos120° = - 0,5, получаем:
75 = 25+x²-10x·(-0,5)
25+x²+5x-75=0
x² + 5x-50 = 0 решаем полученное квадратное уравнение.
D=25-4 · 1 · (-50) = 25+200 = 225 = 15²
x₁ =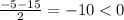
x₂ =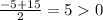
ВС = 5 см - расстояние на карте.
3) На основании соотношений:
1 см - 20 км
5 см - х км
Получаем пропорцию:
1 : 20 = 5 : х ( можно записать и так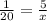 )
)
Решаем:
x = 20 · 5 : 1
x = 100 км - расстояние на местности
ответ: 100 км