Al-бісектриса прямокутного трикутника авс, у якого

В решении.

Объяснение:

Выберите функции, графики которых параллельны, пересекаются или совпадают, ответ обоснуйте:

Уравнение линейной функции: у = kx + b.

A) у=6 и у=х+6

Прямые пересекутся, так как k₁ ≠ k₂.

B) 2у=4х+6 и у=2х+3

2у=4х+6/2

у=2х+3  и у=2х+3, это практически одна и та же функция.

Прямые сольются, так как k₁ =  k₂,   b₁ =  b₂.

C) у= -4х-4 и у= -х-8

Прямые пересекутся, так как k₁ ≠ k₂

D) у= -3х+5 и у= -3х+6

Прямые параллельны, так как k₁ = k₂, а b₁ ≠  b₂.

E) у=0,5х+3 и у=2х+3

Прямые пересекутся, так как k₁ ≠  k₂.

а) 10

б) 120

Объяснение:

Пусть а - арифметическая прогрессия, учитывающая 1 шар как 1 единицу. Тогда, d = 1, так как в каждом ряду количество шаров на 1 больше, чем в предыдущем, а1 = 1, так так в первом ряду 1 шар.

а) S(n) =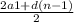 * n = 55

Подставим а1 и d:

* n = 55

(2 + (n - 1)) * n / 2 = 55

(2 + (n - 1)) * n = 110

(2 + n - 1) * n = 110

(n + 1) * n = 110

+ n - 110 = 0

D = 1 - 4 * 1 * (-110) = 441 =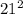

n1 = (-1 - 21) / 2 = -11, не удовлетворяет условию

n2 = (-1 + 21) / 2 = 10

То есть, n = 10.

б) S (15) =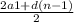 * n = 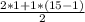* 15 = (2 + 14) * 15 / 2 = 120