Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Х
Химия
Д
Другие предметы
Н
Немецкий язык
Б
Беларуская мова
М
Музыка
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
У
Українська література
Р
Русский язык
Ф
Французский язык
П
Психология
О
Обществознание
А
Алгебра
М
МХК
Г
География
И
Информатика
П
Право
А
Английский язык
Г
Геометрия
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
foximmortal
30.09.2021 19:42 •
Алгебра
Алгебра
1/(n+1) + 1/(n+2) + ... + 1/(2n) > 1/2; при n>=2
Показать ответ
Ответ:
Darya789
11.02.2021 23:38
Для
выполнено неравенство
, причем равенство возможно в единственном случае: при
. Поэтому
.
0,0
(0 оценок)
Популярные вопросы: Алгебра
oleglebedev90
26.06.2022 07:14
7. Куплено несколько одинаковых книг и одинаковых тетрадей. За книги заплачено 1072 рубля. Сколь- ко куплено книг, если цена одной книги более чем на 100 рублей превосходит...
настя7595
04.03.2023 08:31
Практическая работа.решите 1 и 2 вариант...
aleksaprincessa
15.02.2022 02:53
Туристы пешком x км и проехали на автобусе 5x ем. на автобусе туристы проехали на 60 км больше;...
katerinatumasjp02dx5
23.10.2021 11:23
Знайдіть екстремуми функції f(x) = 2х3 + 3х2 - 36хT...
missshapliko20
08.06.2022 00:49
Знайдіть суму перших десяти членів арифметичної прогресії якщо...
hbkkb
25.03.2023 09:37
Корнем уравнения 1/3х = 6 является...
madamnowiczkai
24.02.2020 01:34
Решите уравнение х+9/7-х2=2 , 8+7х=9х+4, х+9/7-х мне очень нужно...
samuray99
21.09.2022 22:56
3. Упростите выражение у2(у4 + у − 2) − у(у5 + 1) + 2у2 − у3 и найдите его значение при у = −1/7....
ighjkhh
19.09.2020 04:07
1. Указать особенности расположения прямых на плоскости и сделать чертеж: 1)x=0 2)5x=y 3)y+7=0 2. Среди данных прямых выбрать пары: а) пересекающихся прямых; б) совпадающих...
PisarenkoEV1
23.12.2020 00:59
В треугольнике ABC проведена высота CD. Известно, что AD=1см,DB=4см,CD=2см. Докажите, что ACB=90°...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Для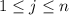 выполнено неравенство
выполнено неравенство 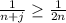 , причем равенство возможно в единственном случае: при
, причем равенство возможно в единственном случае: при 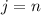 . Поэтому
. Поэтому 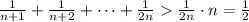 .
.