9^1 mod 8 =1 (9 при делении на 8 даёт в остатке 1), (1+7) mod 8 = 0. Пусть 9^k mod 8 =1. Тогда 9^(k+1) mod 8 = (9*9^k mod 8)=9*(9^k) mod 8 = (9 mod 8)*(9^k mod 8) mod 8 =1.
2, несколько по другому. 3^3 mod 7 = 27 mod 7 = 6. 2^3 mod 7 =1. (6+1) mod 7 = 0. При n=2: 3^5 mod 7 = (6*9) mod 7 = 5. 2^4 mod 7 =(1*2) mod 7 = 2. (5+2) mod 7 = 0. При n=3: Получим, остатки от деления слагаемых на 7 соответственно 3 и 4, а сумма снова делится на 7. При n=4: Остатки будут 6 и 1, как и при n=1. Далее они будут повторяться.
9^1 mod 8 =1 (9 при делении на 8 даёт в остатке 1), (1+7) mod 8 = 0.
Пусть 9^k mod 8 =1. Тогда 9^(k+1) mod 8 = (9*9^k mod 8)=9*(9^k) mod 8 = (9 mod 8)*(9^k mod 8) mod 8 =1.
2, несколько по другому. 3^3 mod 7 = 27 mod 7 = 6. 2^3 mod 7 =1. (6+1) mod 7 = 0.
При n=2: 3^5 mod 7 = (6*9) mod 7 = 5. 2^4 mod 7 =(1*2) mod 7 = 2. (5+2) mod 7 = 0.
При n=3: Получим, остатки от деления слагаемых на 7 соответственно 3 и 4, а сумма снова делится на 7.
При n=4: Остатки будут 6 и 1, как и при n=1. Далее они будут повторяться.
Скорость грузового - 40, легкового - 50
за первый час легковой догонит грузового на 50-40=10 км
за второй на 10+(55-40)=25 км. и тд. каждый час все больше.
Положим, что первый член равен 10, тогда второй - 15 ,третий 20 и т.д.
Сумма членов прогрессии 10,15,20,25... должна равнятся 135
Сумма АП равна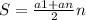
, но т.к. последний член не известен выразим an через a1 и n: 
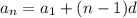и формулу суммы можно переписать в виде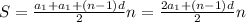 
Подставим известные данные
Решим квадратное уравнение
Положительный корень x = 6 показывает количество членов Ап. т.е. часов за которые легковой догонит грузового