Алгебра: Алгебра 7 класс , заполните табличку .

Алгебра 7 класс , заполните табличку .

Показать ответ

Ответ:

arasukirina6

04.02.2021 16:19

В решении.

Объяснение:

Упростить:

(а² - 1)/(4а² + а - 3);

1) Числитель; разность квадратов, разложить на множители:

(а² - 1) = (а - 1)*(а + 1);

2) Знаменатель; квадратный трёхчлен разложить на множители:

Формула:

ах² + bх + c = а*(х - х₁)*(х - х₂);

Решить квадратное уравнение, вычислить корни:

4а² + а - 3 = 0

D=b²-4ac = 1 + 48 = 49 √D=7

х₁=(-b-√D)/2a

х₁=(-1-7)/8

х₁= -8/8

х₁= -1;

х₂=(-b+√D)/2a

х₂=(-1+7)/8

х₂=6/8

х₂=0,75;

4а² + а - 3 = 4*(х + 1)*(х - 0,75);

3) Записать преобразованные числитель и знаменатель в виде дроби:

((а - 1)*(а + 1))/(4*(х + 1)*(х - 0,75)) =

сократить (разделить) (х + 1) и (х + 1) на (х + 1);

= (а - 1)/(4*(х - 0,75)) =

= (а - 1)/(4а -3). ответ.

0,0(0 оценок)

Ответ:

Dashka6969

19.01.2023 05:36

b1 = 16/3 = 5,33, b2 = -2,66; b3 = 1,33, q = -1/2

Объяснение:

1) Выразим b2 через b1 =>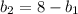 $b_{2} = 8 - b_{1}$ ;

2) Подставим во второе уравнение системы и упростим. Получится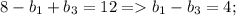 $8 - b_{1} + b_{3} = 12 = b_{1} - b_{3} = 4;$

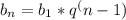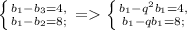
3) Запишем новую систему и разложим по формуле геометрической прогрессии: $b_{n} = b_{1} * q^(n-1)$ => $\left \{ {{b_{1} - b_{3} = 4, } \atop {b_{1} - b_{2} = 8;}} \right. = \left \{ {{b_{1} - q^2 b_{1} = 4, } \atop {b_{1} - qb_{1} = 8;}}$

4) Разделим оба уравнения друг друга т.к. b1-q*b1 не равно 0. Вынесем общий множитель, сократим, разложим числитель по ФСУ, сократим и получим знаменатель геометрической прогрессии

$\frac{b_{1} - q^2b_{1}}{b_{1} - qb_{1}} = \frac{4}{8} = \frac{b_{1}(1 - q^2)}{b_{1}(1 - q)} = \frac{1}{2} = \frac{(1 + q)(1 - q)}{(1 - q)} = \frac{1}{2} = 1 + q = \frac{1}{2};\\q = -\frac{1}{2}$