Поскольку прямая проходит через точку , то подставив её координаты в уравнение прямой получим:
Значит наша прямая имеет вид
В точках пересечения значения функций должны быть равными
По т. Виета: , значит
P.S.: Тут хорошо бы еще отметить, что поскольку в условии заранее известно, что прямая пересекает параболу в двух точках, то проверять условие наличия корней у квадратного уравнения не требуется. Так же, в последней строчке решения, при сокращении дроби на по идее необходимо убедиться что , однако в этом случае точка пересечения будет только одна, поэтому подобные сокращение можно смело называть легальным)
Так как не написано, как именно измениться увеличится на 8 или уменьшится на 8. То разберём 2 случая.
1) Составим систему уравнений для первого случая из трёх взаимо-связанных уравнений:1) x+y=11
2) x^2+y^2=z
3) (x+4)^2+(y-4)^2=z+8
Подставим z из 2-ого уравнения в 3-ье
(x+4)^2+(y-4)^2=x^2+y^2+8
x^2+8x+16+y^2-8y+16=x^2+y^2+8
x^2 и y^2 взаимно уничтожаются
8x-8y+32=8
8x-8y=8-32
8(x-y)=-24
Рассмотрим 1-ое уравнение
x+y=11
Решим относительно x
x=11-y
Вернемся к уравнению 8(x-y)=-24 и вместо x подставим (11-y)
8((11-y)-y)=-24
8(11-2y)=-24
Обе части уравнения делим на 8
11-2y=-3
-2y=-3-11
-2y=-14
y=7
Подставим вместо y число 7 в 1-ое уравнение и найдём x
x=11-7=4
2) Составим систему уравнений для второго случая из трёх взаимо-связанных уравнений:1) x+y=11
2) x^2+y^2=z
3) (x+4)^2+(y-4)^2=z-8
Подставим z из 2-ого уравнения в 3-ье
(x+4)^2+(y-4)^2=x^2+y^2-8
x^2+8x+16+y^2-8y+16=x^2+y^2-8
x^2 и y^2 взаимно уничтожаются
8x-8y+32=-8
8x-8y=-8-32
8(x-y)=-40
Рассмотрим 1-ое уравнение
x+y=11
Решим относительно x
x=11-y
Вернемся к уравнению 8(x-y)=-40 и вместо x подставим (11-y)
8((11-y)-y)=-40
8(11-2y)=-40
Обе части уравнения делим на 8
11-2y=-5
-2y=-5-11
-2y=-16
y=8
Подставим вместо y число 8 в 1-ое уравнение и найдём x
x=11-8=3
Следовательно в первом случае это число 47, а во втором 38.ответ: 47, так как таких чисел несколько, а в ответ нужно написать большее.Объяснение:
Объяснение:
Пусть прямая задается уравнением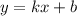
Поскольку прямая проходит через точку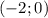
, то подставив её координаты в уравнение прямой получим: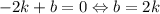 
Значит наша прямая имеет вид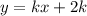
В точках пересечения значения функций должны быть равными
По т. Виета: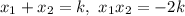
, значит
P.S.: Тут хорошо бы еще отметить, что поскольку в условии заранее известно, что прямая пересекает параболу в двух точках, то проверять условие наличия корней у квадратного уравнения не требуется. Так же, в последней строчке решения, при сокращении дроби на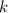
по идее необходимо убедиться что 
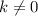, однако в этом случае точка пересечения будет только одна, поэтому подобные сокращение можно смело называть легальным)