Заметим, что при левая и правая часть уравнения обращается в 0. Значит, число 0 является корнем этого уравнения.
Предположим, что . Тогда, мы можем разделить обе части равенства на . Получим:
Рассмотрим левую часть.
Вспомним, что функция вида является возрастающей на всей области определения, то есть на множестве действительных чисел. Тогда и функция является возрастающей. Сумма возрастающих функций также является возрастающей.
Применительно к данному уравнению можно записать: функции , , ..., возрастают, тогда и функции , , ..., также возрастают, а значит возрастает и их сумма.
Таким образом, функция возрастает. Это означает, что каждое свое значение она принимает только в одной точке.
Следовательно, уравнение может иметь не более одного решения.
Решение уравнения легко подбирается: . Действительно, сумма коэффициентов в левой части уравнения равна 44:
В силу сказанного выше, других корней у уравнения нет.
x ∈ [⅔; 6)
Объяснение:
ОДЗ:
Возводим в квадрат обе части уравнения:
(√(x + 3) + √(3x - 2))² < 7²
Решаем:
x + 3 + 2√((x + 3)(3x-2)) + 3x - 2 < 49
4x + 1 + 2√(3x² + 7x - 6) < 49
2√(3x² + 7x - 6) < 48 - 4х | :2
√(3x² + 7x - 6) < 24 - 2x
Имеем два случая:
Если 1) 24 - 2x < 0, то нет корней;
2) 24 - 2x ≥ 0
(√(3x² + 7x - 6))² < (24 - 2x)² при 24 - 2x ≥ 0
ОДЗ: 3x² + 7x - 6 ≥ 0; (x+3)*(3x - 2) ≥ 0
+ - +
------•------•------>
-3 ⅔
ОДЗ: x ∈ (-∞; -3] ∪ [⅔; +∞)
Решаем далее:
3x² + 7x - 6 < 4x² - 96x + 576
-x² + 103x - 582 < 0
(x - 6)*(x - 97) > 0 *корни уравнения x² - 103x + 582 = 0 были найдены по т-ме Виета
+ - +
------о------о------>
6 97
х ∈ (-∞; 6) ∪ (97; +∞)
Так как мы взяли 24 - 2х ≥ 0, то: 24 ≥ 2x; x ≤ 12.
х ∈ (-∞; 6) ∪ (97; +∞) при x ≤ 12, то у нас решение первого нер-ва: х ∈ (-∞; 6).
В итоге, решением заданного по условию неравенства является решение 1-го полученного неравенства и ограничения начального неравенства:
х ∈ (-∞; 6) при x ∈ [⅔; +∞)
Пересечением данных неравенств является интервал: x ∈ [⅔; 6). Это и будет ответом.
Заметим, что при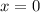
левая и правая часть уравнения обращается в 0. Значит, число 0 является корнем этого уравнения.
Предположим, что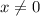
. Тогда, мы можем разделить обе части равенства на 
. Получим:
Рассмотрим левую часть.
Вспомним, что функция вида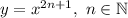
является возрастающей на всей области определения, то есть на множестве действительных чисел. Тогда и функция 
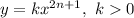является возрастающей. Сумма возрастающих функций также является возрастающей.
Применительно к данному уравнению можно записать: функции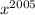
, 
, ..., 
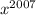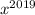возрастают, тогда и функции 
, 
, ..., 
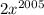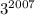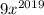также возрастают, а значит возрастает и их сумма.
Таким образом, функция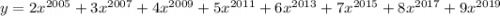
возрастает. Это означает, что каждое свое значение она принимает только в одной точке.
Следовательно, уравнение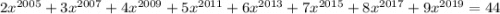
может иметь не более одного решения.
Решение уравнения легко подбирается: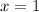
. Действительно, сумма коэффициентов в левой части уравнения равна 44:
В силу сказанного выше, других корней у уравнения нет.
ответ: 0; 1