Если я правильно понял задачу, то ладьи нужно расставить по шахматным правилам, т.е. белые не бьют черных, но при этом фигуры одного цвета могут атаковать друг друга.
Всего возможных расстановок 64*63*62*61 (Сначала было свободно 64 поля, т.е. число возможных расстановок одной ладьи равно 64. После постановки первой ладьи свободными остались 63 поля. Соответственно, число которыми можно расставить две ладьи, равно 64*63. Продолжая рассуждения до 4-ой ладьи приходим к числу 64*63*62*61). Найдем количество расстановок, удовлетворяющих условию. Пусть сначала ставятся две белые ладьи, а затем две черные. Ладья примечательна тем, что из любого поля доски обстреливает ровно 14 клеток (Легко показать. Ладья занимает одно из полей на одной из вертикалей и обстреливает остальные семь. Аналогично для горизонталей. В сумме 7 + 7 = 14). Возможны два случая: 1) Обе белые ладьи не атакуют друг друга. Тогда количество необстреливаемых ими полей равно 36 (Одна ладья обстреливает 14 полей, плюс занимает одно поле - всего 15. Вторая ладья также обстреливает 14 полей, однако из них 2 поля уже обстреливает первая ладья. Плюс поле, на котором стоит вторая ладья. В сумме 14 + 1 + 12 + 1 = 28. Тогда необстреливаемых полей 64 - 28 = 36). Соответственно число таких расстановок равно 64*49*36*35 (Первую ладью ставим 64-мя Под обстрел попадают 14 полей плюс поле, на которое встала первая ладья. Итого 64 - 14 -1 = 49 полей для второй ладьи. Необстреленных полей для третьей ладьи 36. И для четвертой ладьи 35 полей, так как одно из 36-и занято). 2) Обе белые ладьи атакуют друг друга. Необстреливаемых полей теперь 42 (Рассмотрим линию, на которой стоят обе ладьи. Понятно, что вся эта линия, т.е. 8 полей, заняты. Плюс дважды семь полей, которые обстреливаются по перпендикулярному данной линии направлению. Итого занято 8 + 7 + 7 = 22 поля. Тогда свободно 64 - 22 = 42 поля). Тогда число расстановок таких расстановок равно 64*14*42*41 (Первую ладью ставим 64-мя Под обстрел попало 14 полей, значит для второй ладьи всего 14 мест. Необстреленных полей для третьей ладьи 42. И для четвертой ладьи 41 поле, так как одно из 42-х занято). Значит вероятность равна (64*49*36*35 + 64*14*42*41)/(64*63*62*61) ≈ 0,3603 = 36,03%.
Приведу ответ и на тот случай, если цвет не важен и ладьи просто не должны бить друг друга. ответ (64*49*36*25)/(64*63*62*61) ≈ 0,1851 = 18,51%.
a) Вероятность взять один синий карандаш, равна 5/9. В коробке останется 8 карандашей. Вероятность взять второй синий карандаш, равна 4/8 = 1/2, вероятность взять третий сини карандаш равна 3/7. По теореме умножения, 5/9 * 1/2 * 3/7 = 5/42
Аналогично вероятность взять один красный карандаш равна 4/9, второй красный карандаш - 3/8, третий красный карандаш - 2/7. По теореме умножения, 4/9 * 3/8 * 2/7 = 1/21
По теореме сложения, вероятность взять 3 карандаша одинакового цвета равна 5/42 + 1/21 = 5/42 + 2/42 = 7/42 = 1/6
б) Всего всевозможных исходов: из них нужно взять 2 синих и 1 красный карандаш, таких у нас . Вероятность того, что среди отобранных 3 карандаша 2 синих и 1 красный карандаш, равна 40/84 = 10/21
c) Вероятность того, что среди наугад выбранных 3 карандаша нет синего цвета, равна 1/21 (посчитали в пункте а), тогда вероятность того, что среди них будет хотя бы 1 карандаш синий, равна 1 - 1/21 = 20/21
Всего возможных расстановок 64*63*62*61 (Сначала было свободно 64 поля, т.е. число возможных расстановок одной ладьи равно 64. После постановки первой ладьи свободными остались 63 поля. Соответственно, число которыми можно расставить две ладьи, равно 64*63. Продолжая рассуждения до 4-ой ладьи приходим к числу 64*63*62*61).
Найдем количество расстановок, удовлетворяющих условию. Пусть сначала ставятся две белые ладьи, а затем две черные. Ладья примечательна тем, что из любого поля доски обстреливает ровно 14 клеток (Легко показать. Ладья занимает одно из полей на одной из вертикалей и обстреливает остальные семь. Аналогично для горизонталей. В сумме 7 + 7 = 14).
Возможны два случая:
1) Обе белые ладьи не атакуют друг друга. Тогда количество необстреливаемых ими полей равно 36 (Одна ладья обстреливает 14 полей, плюс занимает одно поле - всего 15. Вторая ладья также обстреливает 14 полей, однако из них 2 поля уже обстреливает первая ладья. Плюс поле, на котором стоит вторая ладья. В сумме 14 + 1 + 12 + 1 = 28. Тогда необстреливаемых полей 64 - 28 = 36). Соответственно число таких расстановок равно 64*49*36*35 (Первую ладью ставим 64-мя Под обстрел попадают 14 полей плюс поле, на которое встала первая ладья. Итого 64 - 14 -1 = 49 полей для второй ладьи. Необстреленных полей для третьей ладьи 36. И для четвертой ладьи 35 полей, так как одно из 36-и занято).
2) Обе белые ладьи атакуют друг друга. Необстреливаемых полей теперь 42 (Рассмотрим линию, на которой стоят обе ладьи. Понятно, что вся эта линия, т.е. 8 полей, заняты. Плюс дважды семь полей, которые обстреливаются по перпендикулярному данной линии направлению. Итого занято 8 + 7 + 7 = 22 поля. Тогда свободно 64 - 22 = 42 поля). Тогда число расстановок таких расстановок равно 64*14*42*41 (Первую ладью ставим 64-мя Под обстрел попало 14 полей, значит для второй ладьи всего 14 мест. Необстреленных полей для третьей ладьи 42. И для четвертой ладьи 41 поле, так как одно из 42-х занято).
Значит вероятность равна (64*49*36*35 + 64*14*42*41)/(64*63*62*61) ≈ 0,3603 = 36,03%.
Приведу ответ и на тот случай, если цвет не важен и ладьи просто не должны бить друг друга. ответ (64*49*36*25)/(64*63*62*61) ≈ 0,1851 = 18,51%.
a) Вероятность взять один синий карандаш, равна 5/9. В коробке останется 8 карандашей. Вероятность взять второй синий карандаш, равна 4/8 = 1/2, вероятность взять третий сини карандаш равна 3/7. По теореме умножения, 5/9 * 1/2 * 3/7 = 5/42
Аналогично вероятность взять один красный карандаш равна 4/9, второй красный карандаш - 3/8, третий красный карандаш - 2/7. По теореме умножения, 4/9 * 3/8 * 2/7 = 1/21
По теореме сложения, вероятность взять 3 карандаша одинакового цвета равна 5/42 + 1/21 = 5/42 + 2/42 = 7/42 = 1/6
б) Всего всевозможных исходов: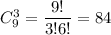
из них нужно взять 2 синих и 1 красный карандаш, таких у нас 
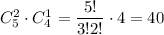. Вероятность того, что среди отобранных 3 карандаша 2 синих и 1 красный карандаш, равна 40/84 = 10/21
c) Вероятность того, что среди наугад выбранных 3 карандаша нет синего цвета, равна 1/21 (посчитали в пункте а), тогда вероятность того, что среди них будет хотя бы 1 карандаш синий, равна 1 - 1/21 = 20/21