Объяснение: Для умножения многочлена на многочлен существует очень легкое правило. Чтобы умножить два многочлена между собой, надо каждый член первого многочлена умножить на каждый член второго многочлена. После это полученные произведения сложить и привести подобные.
2. А
Объяснение: У вырази a*b е два множники, ''a''*b називається першим множником, а*''b'' називається другим множником.
3. В
Объяснение: Спрощуючи даний вираз, згрупуємо окремо числові та буквені множники.
4. Г
5. Б
Объснение: Коэффицие́нт «совместно» + «производящий») — термин, обозначающий числовой множитель при буквенном выражении, множитель при той или иной степени неизвестного, или постоянный множитель при переменной величине.
Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру уравнение в действительных корнях.
Рассмотрим функцию . Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию . Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
1. Б
Объяснение: Для умножения многочлена на многочлен существует очень легкое правило. Чтобы умножить два многочлена между собой, надо каждый член первого многочлена умножить на каждый член второго многочлена. После это полученные произведения сложить и привести подобные.
2. А
Объяснение: У вырази a*b е два множники, ''a''*b називається першим множником, а*''b'' називається другим множником.
3. В
Объяснение: Спрощуючи даний вираз, згрупуємо окремо числові та буквені множники.
4. Г
5. Б
Объснение: Коэффицие́нт «совместно» + «производящий») — термин, обозначающий числовой множитель при буквенном выражении, множитель при той или иной степени неизвестного, или постоянный множитель при переменной величине.
6. А
Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру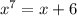
уравнение в действительных корнях.
Рассмотрим функцию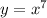
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию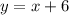
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение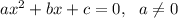
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.