Пусть первоначальная масса сплава равна М. Тогда содержание меди в сплаве было .
К сплаву добавили 20 кг меди, масса сплава стала М+20 кг. Тогда содержание меди в сплаве стало . При этом содержание меди увеличилось на 20%.
(15 + 0,2M)(M + 20) = 35 M
15M + 0,2M² + 300 + 4M - 35M = 0
0,2M² - 16M + 300 = 0 | × 5
M² - 80M + 1500 = 0
(M - 50)(M - 30) = 0
1) M - 50 = 0; M = 50 > 40 - не подходит под условие
2) M - 30 = 0; M = 30 кг
ответ : 30 кг
=================================
Проверка :
- первоначальное содержание меди в сплаве.
- содержание меди после добавления 20 кг.
70% - 50% = 20%
ух сколько ненужных лишних накруток
снимает нечетные степени , совершенно очевидно, что если число больше другого, то и в 9-й степени они будут также соотносится
∛x + 3^(x+1) - 3 > ∛x + 9^x - 3^x
∛x взаимно уничтожатся , никаких ограничений на корни нечетной степени неи надо (на четной надо)
9^x = (3^x)^2
3^x=t
3t - 3 > t^2 - t
t^2 - 4t + 3 < 0
D = 16-12 = 4
t12=(4+-2)/2 = 1 3
(t-1)(t-3) < 0
метод интервалов
(1) (3)
t∈(1 3)
t>1 3^x>1 3^x>3^0 x>0
t<3 3^x < 3 x < 1
x∈(0, 1)
Пусть первоначальная масса сплава равна М. Тогда содержание меди в сплаве было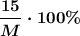 .
.
К сплаву добавили 20 кг меди, масса сплава стала М+20 кг. Тогда содержание меди в сплаве стало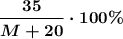 . При этом содержание меди увеличилось на 20%.
. При этом содержание меди увеличилось на 20%.
(15 + 0,2M)(M + 20) = 35 M
15M + 0,2M² + 300 + 4M - 35M = 0
0,2M² - 16M + 300 = 0 | × 5
M² - 80M + 1500 = 0
(M - 50)(M - 30) = 0
1) M - 50 = 0; M = 50 > 40 - не подходит под условие
2) M - 30 = 0; M = 30 кг
ответ : 30 кг
=================================
Проверка :
70% - 50% = 20%
ух сколько ненужных лишних накруток
снимает нечетные степени , совершенно очевидно, что если число больше другого, то и в 9-й степени они будут также соотносится
∛x + 3^(x+1) - 3 > ∛x + 9^x - 3^x
∛x взаимно уничтожатся , никаких ограничений на корни нечетной степени неи надо (на четной надо)
9^x = (3^x)^2
3^x=t
3t - 3 > t^2 - t
t^2 - 4t + 3 < 0
D = 16-12 = 4
t12=(4+-2)/2 = 1 3
(t-1)(t-3) < 0
метод интервалов
(1) (3)
t∈(1 3)
t>1 3^x>1 3^x>3^0 x>0
t<3 3^x < 3 x < 1
x∈(0, 1)