1)а) x²+3x-4=0
Коэффициенты: старший = 1
Второй = 3
Свободный член = -4
б)x²+14x=0
Второй = 14
Свободный член = 0
2) а)x² - + =0
б)x² - 3x - 12 = 0
3) а) 0; -5
б) -3 ; 3
в) √5,5 ; -√5,5
Объяснение:
1)
a. (x-1)(x+4)=0
x²+4x-x-4=0
x²+3x-4=0
Коэффициенты: старший = a = 1
Второй = b = 3
Свободный член = c = -4
b. 12 - 6(x+3) -7x = (x-2)(x+3)
12 - 6x - 18 - 7x = x²+3x-2x-6
-6-13x = x²+x-6
-6-13x -x²-x+6=0
-x²-14x=0 (домножили на -1)
x²+14x=0
Второй = b = 14
Свободный член = c = 0
2.
a) -15x²+4x-2=0 разделим на -15
x² - + =0
б) 12 - x² + 3x = 0
- x² + 3x+12=0 домножим на -1
x² - 3x - 12 = 0
3.
a) x²+5x =0
x(x+5) =0
Произведение равно 0, когда один из множителей равен 0
x1=0 или x+5=0
x2= -5
б) x² - 9 =0
x²=9
x1 = √9 = 3
x2 = -√9 = -3
в) -2x²+11=0
-2x²=-11 разделим на -2
x² = 5,5
x1=√5,5
x2= -√5,5
3x⁷-3x⁶ 3x⁶+3x⁵+3x⁴-x³-x²-x -1
_3x⁶-4x⁴+6
3x⁶-3x⁵
_3x⁵-4x⁴+6
3x⁵-3x⁴
_-x⁴+6
-x⁴+x³
_-x³+6
-x³+x²
_-x²+6
-x²+x
_-x+6
-x+1
5 - остаток
1)а) x²+3x-4=0
Коэффициенты: старший = 1
Второй = 3
Свободный член = -4
б)x²+14x=0
Коэффициенты: старший = 1
Второй = 14
Свободный член = 0
2) а)x² -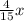 +
+ 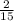 =0
=0
б)x² - 3x - 12 = 0
3) а) 0; -5
б) -3 ; 3
в) √5,5 ; -√5,5
Объяснение:
1)
a. (x-1)(x+4)=0
x²+4x-x-4=0
x²+3x-4=0
Коэффициенты: старший = a = 1
Второй = b = 3
Свободный член = c = -4
b. 12 - 6(x+3) -7x = (x-2)(x+3)
12 - 6x - 18 - 7x = x²+3x-2x-6
-6-13x = x²+x-6
-6-13x -x²-x+6=0
-x²-14x=0 (домножили на -1)
x²+14x=0
Коэффициенты: старший = a = 1
Второй = b = 14
Свободный член = c = 0
2.
a) -15x²+4x-2=0 разделим на -15
x² -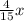 +
+ 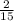 =0
=0
б) 12 - x² + 3x = 0
- x² + 3x+12=0 домножим на -1
x² - 3x - 12 = 0
3.
a) x²+5x =0
x(x+5) =0
Произведение равно 0, когда один из множителей равен 0
x1=0 или x+5=0
x2= -5
б) x² - 9 =0
x²=9
x1 = √9 = 3
x2 = -√9 = -3
в) -2x²+11=0
-2x²=-11 разделим на -2
x² = 5,5
x1=√5,5
x2= -√5,5