Это квадратичная функция , ограничений на переменную х не накладываются , поэтому
- область определения функции .
Графиком квадратичной функции является парабола, причём, т.к. коэффициент перед х² равен -1<0 , то ветви параболы направлены вниз , и выше вершины в точке (0;5) графика существовать не будет . Поэтому самое максимальное значение , которое принимает заданная функция равно f(x)=5 . Поэтому область значений функции
Cмотри рисунок .
Графиком этой функции является график функции у=|x| ( угол , ветви вверх ) сдвинутый вдоль оси ОХ на 2 единицы влево и вдоль оси ОУ на 2 единицы вверх .
ООФ:
ОЗФ:
Смотри рисунок .
Под знаком квадратного корня может быть записано только неотрицательное выражение.
Решение.
Это квадратичная функция , ограничений на переменную х не накладываются , поэтому
Графиком квадратичной функции является парабола, причём, т.к. коэффициент перед х² равен -1<0 , то ветви параболы направлены вниз , и выше вершины в точке (0;5) графика существовать не будет . Поэтому самое максимальное значение , которое принимает заданная функция равно f(x)=5 . Поэтому область значений функции
Cмотри рисунок .
Графиком этой функции является график функции у=|x| ( угол , ветви вверх ) сдвинутый вдоль оси ОХ на 2 единицы влево и вдоль оси ОУ на 2 единицы вверх .
ООФ: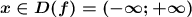
ОЗФ: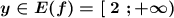
Смотри рисунок .
Под знаком квадратного корня может быть записано только неотрицательное выражение.
ООФ: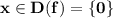 - это множество из одного элемента .
- это множество из одного элемента .
ОЗФ: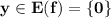
***
квадратное уравнение — это уравнение вида ax² + bx + c = 0,
где
a — первый коэффициент, не равный нулю
b — второй коэффициент
c — свободный член.
решаем с дискриминанта:
1) x² - x - 90 = 0
a = 1, b = -1, c = -90
D = b² - 4ac = (-1)² - 4 · 1 · (-90) = 361 >0
т.к. дискриминант больше нуля, то квадратное уравнение имеет два различных действительных корня
=>
X₁ = (-b+√D) / 2a = ( -(-1) + √361 ) / 2 · 1 = 1 + 19 / 2 = 20/2 = 10
X₂ = (-b-√D) / 2a = ( -(-1) - √361 ) / 2 · 1 = 1 - 19 / 2 = -18/2 = -9
2) x² + 6x + 9 = 0
a = 1, b = 6, c = 9
D = b² - 4ac = (6)² - 4 · 1 · 9 = 36 - 36 = 0
т.к. дискриминант равен нулю, то квадратное уравнение имеет только один действительный корень
=>
X₁,₂ = (-b±√D) / 2a = ( (-6) ±√D ) / 2
3) 5x² + 4x + 7 = 0
a = 5, b = 4, c = 7
D = b² - 4ac = (4)² - 4 · 5 · 7 = 16 - 140 = - 124 < 0
т.к. дискриминант меньше нуля, значит не существует вещественных корней, а только комплексные корни
4) x² + 2x - 35 = 0
a = 1, b = 2, c = -35
D = b² - 4ac = (2)² - 4 · 1 · (-35) = 4 - (-140) = 4 + 140 = 144
т.к. дискриминант больше нуля, то квадратное уравнение имеет два различных действительных корня
=>
X₁ = (-b+√D) / 2a = ( (-2) + √144 ) / 2 · 1 = (-2 + 12) / 2 = 10/2 = 5
X₂ = (-b-√D) / 2a = ( (-2) - √144 ) / 2 · 1 = (-2 - 12) / 2 = -14/2 = -7