Автомобіль мав проїхати 325 км. Проїхавши цієї відстані, автомобіль зменшив свою швидкість на 15 км/год Знайдіть швидкість автомобіля на кожній ділянці руху якщо на весь шлях було витрачено 5 год
1. , интеграл табличный и равняется , тогда исходный равняется , произведение констант — тоже константа, поэтому решением будет , что соответствует второму варианту ответа.
2. Область , ограниченная указанными кривыми , , и , показана на приложенном рисунке. Получается, что задают два неравенства, и . Первое неравенство задаёт подынтегральную функцию, притом напрямую (так как левая часть неравенства равна нулю), а второе — пределы интегрирования.
(Так получается, ибо — табличный интеграл, равный , а затем для определённого интегрирования применяется формула Ньютона-Лейбница, то есть , при известном , то есть , притом константа в таком случае игнорируется.)
Полученный результат соответствует третьему варианту ответа.
Областью определения выражения являются все вещественные числа, кроме тех, при которых выражение не определено. В данном случае нет вещественных чисел, при которых выражение было бы неопределенным.
Запись в виде интервала:
(
−
∞
;
∞
)
Нотация построения множества:
{
x
|
x
∈
R
}
Каждому значению
x
соответствует одно значение
y
. Выберем несколько значений
x
из области определения. Наиболее полезно выбрать значения, в окрестности
1. 2)
2. 3)
Объяснение:
1.
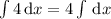, интеграл 
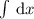табличный и равняется 
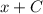, тогда исходный равняется 
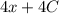, произведение констант — тоже константа, поэтому решением будет 
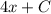, что соответствует второму варианту ответа.
2. Область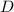
, ограниченная указанными кривыми 
, 
, 
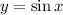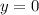и 
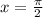, показана на приложенном рисунке. Получается, что 
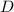задают два неравенства, 
и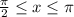 
. Первое неравенство задаёт подынтегральную функцию, притом напрямую (так как левая часть неравенства равна нулю), а второе — пределы интегрирования.
(Так получается, ибо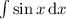
— табличный интеграл, равный 
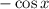, а затем для определённого интегрирования применяется формула Ньютона-Лейбница, то есть 
, при известном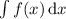 
, то есть 
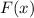, притом константа в таком случае игнорируется.)
Полученный результат соответствует третьему варианту ответа.
Найдем вершину модуля. В данном случае, вершиной
y
=
|
x
−
3
|
является
(
3
;
0
)
.Введите задачу...
Алгебра Примеры
Популярные задачи Алгебра График y=|x-3|
y
=
|
x
−
3
|
Найдем вершину модуля. В данном случае, вершиной
y
=
|
x
−
3
|
является
(
3
;
0
)
.
Нажмите, чтобы увидеть больше шагов...
(
3
;
0
)
Областью определения выражения являются все вещественные числа, кроме тех, при которых выражение не определено. В данном случае нет вещественных чисел, при которых выражение было бы неопределенным.
Запись в виде интервала:
(
−
∞
;
∞
)
Нотация построения множества:
{
x
|
x
∈
R
}
Каждому значению
x
соответствует одно значение
y
. Выберем несколько значений
x
из области определения. Наиболее полезно выбрать значения, в окрестности
x
значения вершины абсолютного значения.