Автомобиль с некоторой постоянной скоростью путь от А до В длиной 240 км. Возвращаясь обратно, он половину пути с той же скоростью, а затем увеличил её на 10 км/ч. В результате на обратный путь было затрачено на 25 ч меньше, чем на путь от А до В. С какой скоростью шёл автомобиль из А в В?
Пусть скорость автомобиля равна х км/ч. Скорость после увеличения равна (x+10) км/ч. Автомобиль за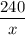
ч из пункта А в пункт В. За первую половину пути из пункта В в пункт А он проехал 
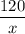часов, а оставшееся вреся - 
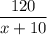часов. Зная, что на обратный путь автомобиль затратил 25 ч меньше, чем на путь от А в В, составим и решим уравнение:
Домножим левую и правую части уравнения на x(x+10)/5
Однако в условии, что-то не так. Расстояние 240 км можно преодолеть намного меньше чем 25 часов.. Не такое уж и большое расстояние