Пусть x - скорость работы первого, y - скорость работы второго, при объеме работы равном 1(не важно чему именно равен объем работы так как вычисления идет относительно него, то есть он сократится в итоге. Если хочешь можешь использовать вместо него третью переменную). Время затрачиваемое на работу первым: 1/x, время затрачеваемое вторым 1/y, время вместе 1/(x+y). По условию: 1/(x+y)=8 3x+12y=0.75 Решим как систему уравнений: 1=8x+8y x+4y=0.25
По условию:
1/(x+y)=8
3x+12y=0.75
Решим как систему уравнений:
1=8x+8y
x+4y=0.25
x=0.25-4y
1=2-32y+8y
1=2-24y
-3=-24y
y=1/24
x=0.25-4y
x=1/12.
Значит, 1/x=12 (часов), 1/y=24 (часов).
Пусть первый может набрать весь текст за х часов, второй за y часов.
Примем всю работу за 1.
Значит, первый за час выполняет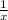 часть работы.
часть работы.
Второй за час выполняет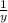 часть работы.
часть работы.
Вместе за час они выполнят: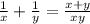
За 8 часов выполнят: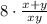 , т.е всю работу 1
, т.е всю работу 1
Первое уравнение:
Если первый оператор будет работать 3 ч,
а второй 12 ч, то они выполнят только 75%=0,75 всей работы.
Второе уравнение:
Решаем систему двух уравнений:
умножим первое уравнение на 3, второе уравнение на 4
Приравниваем левые части:
и подставляем в первое уравнение системы: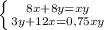
О т в е т. первый может набрать весь текст за 12 часов, второй за 24 часа.