Бабка Маланья
Найти
1.Фразеологизмы
устойчивые
сочетания слов,
имеющие
определенной
значение
2. Пословицы
3. Песни лексика
(характерна для
разговорного
стиля)​

1)

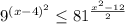
Так как 81 = 9^2, то

Так как основания равны, можно перейти к показателям..

Так как 9 > 1, то функция возрастает, и при переходе знаки остаются.

(x - 4)^2 ≤ x^2 - 12

x^2 - 8x + 16 ≤ x^2 - 12

16 + 12 ≤ 8x

x ≥ 28/8

x ≥ 3,5

ответ: x ∈ [3,5; +oo)

2)

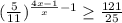
Область определения: x ≠ 0

Так как основания равны, можно перейти к показателям.

Так как  5/11 < 1, то функция убывает, и при переходе знаки меняются.

(3x - 1)/x ≤ -2

(3x - 1)/x + 2 ≤ 0

(3x - 1 + 2x)/x ≤ 0

(5x + 1)/x ≤ 0

Если дробь меньше 0, то числитель и знаменатель имею разные знаки.

а)

{ 5x + 1 ≤ 0

{ x > 0

Решений нет.

б)

{ 5x + 1 ≥ 0

{ x < 0

ответ: x ∈ [-1/5; 0)

x=2; y=-3

Объяснение:

1)   Выражем у из х-   3х-2y=12

                                    2y=-4-x  

2) Подставляем значение у в первое уравнение- 3x- (-4-x)=12

                                                                                       2y=-4-x

3) Раскрываем скобки-    3x+4+x=12

                                            2y=-4-x

4) Слева оставляем только х, а второе слагаемое переносим с противоположным знаком-  4x=12-4

                                                  2y=-4-x

5) Отсюда:  x=2

Теперь подставляем значение х во второе уравнение - 2у=-4-2

                                                                                                  -2y=-6

                                                                                                   y=3