Пусть основание = a см, а боковая сторона = b см. Т.к. нам известен периметр, то можем составить одно уравнение - 2a + 2b = 46. Потом нам известно, что боковая сторона больше основание на 3, т.е. b = a + 3
В итоге получается система уравнений, решив ее получим длины a и b:
Подставляем в первое уравнение значение b из второго уравнения:
Уравнение прямой, проходящей через точки ( -5,-2) и (-2,0) имеет вид y=kx+b:
Уравнение окружности с центром в точке и радиусом, равным R, имеет вид: .
Тогда окружность на рисунке имеет вид:
Если перед корнем берём знак (+), то получаем уравнение верхней полуокружности (y≥0) , а если берём знак (-), то получаем уравнение нижней полуокружности (у≤0) .
Уравнение прямых, проходящих параллельно оси ОХ через точку с координатами (a,b) , имеет вид: у=b .
Аналитически заданная на графике функция имеет вид:
130см
Объяснение:
Пусть основание = a см, а боковая сторона = b см. Т.к. нам известен периметр, то можем составить одно уравнение - 2a + 2b = 46. Потом нам известно, что боковая сторона больше основание на 3, т.е. b = a + 3
В итоге получается система уравнений, решив ее получим длины a и b:
Подставляем в первое уравнение значение b из второго уравнения:
2a + 2(a + 3) = 46
2a + 2a + 6 = 46
4a = 40
a = 10 см
Подставляем значение а во второе уравнение:
b = 10 + 3 = 13 см
Теперь, зная длины сторон, на изи узнать площадь:
a * b = 10 * 13 = 130см
Уравнение прямой, проходящей через точки ( -5,-2) и (-2,0) имеет вид y=kx+b:
Уравнение окружности с центром в точке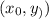 и радиусом, равным R, имеет вид:
и радиусом, равным R, имеет вид: 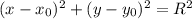 .
.
Тогда окружность на рисунке имеет вид:
Если перед корнем берём знак (+), то получаем уравнение верхней полуокружности (y≥0) , а если берём знак (-), то получаем уравнение нижней полуокружности (у≤0) .
Уравнение прямых, проходящих параллельно оси ОХ через точку с координатами (a,b) , имеет вид: у=b .
Аналитически заданная на графике функция имеет вид: