Решение: Скорость V(t)= x'(t)= 3t²+2; График зависимости -парабола, направленная ветвями вверх, вершиной в точке: t=0 cek, V=2 м/с. зДЕСЬ ЕЁ СКОРОСТЬ МИНИМАЛЬНАЯ. В момент остановки скоростьДОЛЖНА БЫТЬ равна нулю, т.е. V(t) = 0 ⇒ 3t²+2= 0 ⇒ t²=-2/3<0( что невозможно)
продолжает ли точка после момента остановки двигаться в том же направлении или начинает двигаться в противоположном направлениии? ответ: В том же направлении, так как знак скорости не изменился на противоположный.
В начальный момент времени скорость V(0) = 3·0²+2= 2>0, далее скорость возрастает : V(1) = 3·1²+2 = 5 >0
3) Парабола это квадратичная функция, поэтому ответы: A и B
4) ответы Б и В, т.к
x-2>3
-3x<-12
Переносим числа в правую часть с противоположными знаками: (во втором знак неравенства поменяли, т.к делим на отрицательное x)
x>5
x>4
(От 5 до плюс бесконечности)
5) Арифметическая прогрессия - закономерность, при которой каждый член отличается НА сколько-то.
Значит ответ: -2
Т.к 1-ый член равен 7, а разность -1, мы от 7 должны постепенно отнимать -1, (то, есть 10 раз, 7-1=6-1=5..., пока не дойдём до последнего (10-ого члена прогрессии, а 10-ый член прогрессии это -2))
6) Для начала, нужно решить это квадратное уравнение:
4+11x-3=0 (прировняем к нулю)
D=-4ac=121+48=169
x1= -11-13/8= -3
x2= -11+13/8= 0,25
Значит:
4*(x+3)*(x-0,25) (Вот и разложили на трёхчлен)
7)
x+y=3
-x=39
х=3-у (Это мы выразили x, и нужно подставить его во второе уравнение):
у²-(3-у)-39=0
у²-3+у-39=0
у²+у-42=0
D=-4ac=1²-4·(42)=168+1=169
y₁= -1+13/2=6, y₂= -1-13/2= -7
x₁=3-6=-3
x₂=3-(-7)=3+7=10
ответ:(10;-7) и (-3;6)
8) y=-6x+8 (квадратичная функция, значит это парабола)
Вершина этой параболы
(3;-1)
Точки пересечение с осями координат:
ax/y=0
-6x+8=0
x1+x2=6
x1*x2=8
(по теореме Виета)
x1=4 (4;0)
x2=2 (2;0)
ay:x=0
y=8 (0;8)
Значит функция убывает при принадлежности x ( -бесконечности до 3 )
Объяснение:Моменты остановки x(t)=t³+2t, t₀=1
Решение: Скорость V(t)= x'(t)= 3t²+2; График зависимости -парабола, направленная ветвями вверх, вершиной в точке: t=0 cek, V=2 м/с. зДЕСЬ ЕЁ СКОРОСТЬ МИНИМАЛЬНАЯ. В момент остановки скоростьДОЛЖНА БЫТЬ равна нулю, т.е. V(t) = 0 ⇒ 3t²+2= 0 ⇒ t²=-2/3<0( что невозможно)
продолжает ли точка после момента остановки двигаться в том же направлении или начинает двигаться в противоположном направлениии? ответ: В том же направлении, так как знак скорости не изменился на противоположный.
В начальный момент времени скорость V(0) = 3·0²+2= 2>0, далее скорость возрастает : V(1) = 3·1²+2 = 5 >0
3) Парабола это квадратичная функция, поэтому ответы: A и B
4) ответы Б и В, т.к
x-2>3
-3x<-12
Переносим числа в правую часть с противоположными знаками: (во втором знак неравенства поменяли, т.к делим на отрицательное x)
x>5
x>4
(От 5 до плюс бесконечности)
5) Арифметическая прогрессия - закономерность, при которой каждый член отличается НА сколько-то.
Значит ответ: -2
Т.к 1-ый член равен 7, а разность -1, мы от 7 должны постепенно отнимать -1, (то, есть 10 раз, 7-1=6-1=5..., пока не дойдём до последнего (10-ого члена прогрессии, а 10-ый член прогрессии это -2))
6) Для начала, нужно решить это квадратное уравнение:
4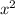
+11x-3=0 (прировняем к нулю)
D=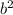
-4ac=121+48=169
x1= -11-13/8= -3
x2= -11+13/8= 0,25
Значит:
4*(x+3)*(x-0,25) (Вот и разложили на трёхчлен)
7)
x+y=3
х=3-у (Это мы выразили x, и нужно подставить его во второе уравнение):
у²-(3-у)-39=0
у²-3+у-39=0
у²+у-42=0
D=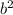
-4ac=1²-4·(42)=168+1=169
y₁= -1+13/2=6, y₂= -1-13/2= -7
x₁=3-6=-3
x₂=3-(-7)=3+7=10
ответ:(10;-7) и (-3;6)
8) y=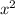
-6x+8 (квадратичная функция, значит это парабола)
Вершина этой параболы
(3;-1)
Точки пересечение с осями координат:
ax/y=0
x1+x2=6
x1*x2=8
(по теореме Виета)
x1=4 (4;0)
x2=2 (2;0)
ay:x=0
y=8 (0;8)
Значит функция убывает при принадлежности x ( -бесконечности до 3 )