Без построения графика функции y=−3x2+12x−4 ответьте на следующие во а) Укажите прямую, служащую осью параболы.

б) Найдите координаты вершины.

в) Куда смотрит парабола (вверх или вниз)?

2. Построить график функции: y=2x2−6x+2

3. Построить график функции: y=−x2+8x−4

4. Найти наибольшее и наименьшее значение функции: y=x2+4x−3 на отрезке [−5;2]

Показать ответ

Ответ:

Iana2010

22.02.2022 12:01

К сожалению, площадь дороги не указаны, поэтому решим задачу в общем виде.

Пусть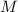 - вместимость грузовика

Пусть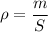 $\displaystyle \rho = \frac{m}{S}$ , где 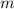- масса щебенки, необходимая на всю отсыпку дорог, 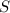- общая площадь дорог.

Наше количество грузовиков высчитаем по такой формуле:

$\displaystyle n=\left[\frac{m}{M}\right]+1$ , то есть это общая масса щебенки, деленная на массу щебенки, влезающей в один грузовик, взятая от всего этого целая часть и плюс один. К примеру, общая масса 120 кг, вместимость грузовика 50кг, 120/50=2.4, [2.4]=2, 2+1=3, оно так и будет: в 2 грузовика по 50 кг и в 1 грузовик 20кг. Будет одно исключение, о котором позже.

не известно, выразим его через известные величины:

$\displaystyle \rho = \frac{m}{S} \Rightarrow m = \rho \cdot S$

$\displaystyle n=\left[\frac{m}{M}\right]+1 \Rightarrow n=\left[\frac{\rho \cdot S}{M}\right]+1$

Теперь подставим все чиселки, за исключением площади, которая должна быть в этой задаче, но куда-то пропала:

$\rho=125$ кг/м²

M=20000 кг/машина

$\displaystyle n=\left[\frac{125 \cdot S}{20000}\right]+1= \left[\frac{S}{32}\right]+1$

Так вот исключением будет случай, когда S кратно 160 м², то есть когда в целой части будет целое число. В этом случае прибавлять лишний грузовик не надо (+1 делать), хотя по жизненной логике это наоборот хорошо, потому что предельно нагружать машины не стоит, так как в таких ситуациях всегда может произойти что-то плохое, но к данной задаче это отношения не имеет, поэтому надо учитывать данную особенность.

0,0(0 оценок)

Ответ: