Билет № 1 1. Дайте определение луча, угла, внешней и внутренней области угла. Какие есть виды углов? Сделайте рисунки.



Билет № 2

1. Дайте определение смежных углов, вертикальных углов, сделайте рисунки. Сформулируйте их свойства.



Билет № 3

1. Дайте определение перпендикулярных прямых. Свойство двух прямых, перпендикулярных третьей. Дайте определение перпендикуляра к прямой.



Билет № 4

1. Дайте определение треугольника. Перечислите виды треугольников (по углам, по сторонам), сделайте рисунки. Сформулируйте теорему о сумме углов треугольника. Дайте определение внешнего угла. Сформулируйте теорему о внешнем угле треугольника.



Билет № 5

1. Дайте определение медианы, биссектрисы, высоты треугольника, сделайте рисунки. Сформулируйте свойства медиан, биссектрис, высот треугольника.

35 км/ч

Объяснение:

Дано:

S₁ = 35 км

S₂ = 34 км

t = 2 ч

Vр = 1 км/ч

V - ?

1)

Заметим, что собственная скорость лодки равна скорости ее движения по озеру:

V₁ = V

Время, затраченное на движение по озеру:

t₁ = S₁ / V₁

или

t₁ = S₁ / V.                  

2)

Время, затраченное на движение по реке.

Заметим, что река впадает в озеро, а это значит, что лодка двигалась против течения: V₂ = V - Vp

t₂ = S₂ / V₂ или

t₂ = S₂ / (V - Vp)

3)

Общее время движения:

t = t₁ + t₂

или

t = S₁ / V₁ + S₂ / (V - Vp)

Подставляем данные и решаем уравнение:

2 = 35 / V + 34 / (V - 1)

2·V·(V-1) = 35·(V-1) + 34·V

2·V² - 2·V = 35·V - 35 +34·V

2·V² - 71·V + 35 = 0

Решая это квадратное уравнение, получаем:

V = (71-69)/4 = 0,5 км/ч (слишком маленькая скорость...)

V = (71+69)/4 = 35 км/ч

а)

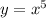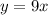Рассмотрим две функции: и . Обе эти функции возрастающие. Тогда и функция, представляющая сумму эти[ функций, то есть функция 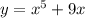будет возрастающей.

Таким образом, в левой части стоит возрастающая функция. Но возрастающая функция принимает каждое свое значение в единственной точке. Это означает, что если найден некоторый корень заданного уравнения, то других корней у уравнения нет.

Корень угадывается достаточно легко: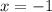 . Проверка:

ответ: -1

б)

Аналогично, каждая из функци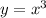й и 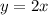возрастает. Значит, возрастает и функция .

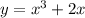Таким образом, уравнение имеет не более одного корня. Этот корень также легко подбирается: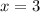 . Проверка:

ответ: 3