Пусть 2-ой рабочий в день изготавливал х детлей, а 1-ый рабочий х+2 детали. 1-ый рабочий изготовил 65 деталей и работал 65/(х+2)дня, 2-ой рабочий изготовил 131-65=66 деталей и работал 66/х дней. 2-ой рабочий работал на 1 день больше, значит 66/х-65/(х+2)=1 приводим общему знаменателю х(х+2)
(66(х+2)-65х)/х(х+2)=1
66х+132-65х=х(х+2)
х+132=х^2+2х
х^2+2х-х-132=0
х^2+х-132=0
Дискриминант Д=1+528=529
корень из Д=23
х1=(-1-23)/2=-12-не может быть отриц
х2=(-1+23)/2=11
2-ой рабочий в день изготавливал 11деталей, а 1-ый рабочий 11+2=13
Пусть 2-ой рабочий в день изготавливал х детлей, а 1-ый рабочий х+2 детали. 1-ый рабочий изготовил 65 деталей и работал 65/(х+2)дня, 2-ой рабочий изготовил 131-65=66 деталей и работал 66/х дней. 2-ой рабочий работал на 1 день больше, значит 66/х-65/(х+2)=1 приводим общему знаменателю х(х+2)
(66(х+2)-65х)/х(х+2)=1
66х+132-65х=х(х+2)
х+132=х^2+2х
х^2+2х-х-132=0
х^2+х-132=0
Дискриминант Д=1+528=529
корень из Д=23
х1=(-1-23)/2=-12-не может быть отриц
х2=(-1+23)/2=11
2-ой рабочий в день изготавливал 11деталей, а 1-ый рабочий 11+2=13
вместе они изготавливали за 1день 11+13=24 детали
№1
а)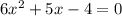
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
б)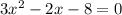
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
№ 2
а)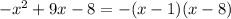
для того чтобы разложить квадратный трёхчлен нужно приравнять его к нулю и найти корни уравнения
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
б)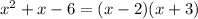
делаем всё по аналогии
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
в)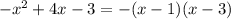
делаем всё по аналогии
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
г)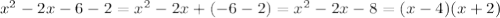
делаем всё по аналогии
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня: