Пусть рыбак поймал всего N рыб. Он их разложил по x рыб в пакет, получилось 17 пакетов - 16 полных и 4 рыбы в последнем. Это значит, что N делится на 16 и на x с остатком 4. Ясно, что x > 4. N = 16x + 4 А когда он разложил те же N рыб по (x-1) рыбы, то у него все пакеты были заполнены. Значит, N делится на (x-1) нацело, и получается неизвестное число пакетов. Представим, что мы уже разложили по x рыб в 16 пакетов, и 4 остались лишние. Вынем из каждого пакета по 1 рыбе. Получится 16 пакетов по (x-1) рыбе и 16 + 4 = 20 рыб остается. Значит, эти 20 рыб делятся на (x-1). 20 = 2*2*5 и имеет делители 1, 2, 4, 5, 10, 20. x - 1 = 4, x = 5, N = 5*16 + 4 = 84 = 4*21 x - 1 = 5, x = 6, N = 6*16 + 4 = 100 = 5*20 x - 1 = 10, x = 11, N = 11*16 + 4 = 180 = 10*18 x - 1 = 20, x = 21, N = 21*16 + 4 = 340 = 20*17
Он их разложил по x рыб в пакет, получилось 17 пакетов -
16 полных и 4 рыбы в последнем.
Это значит, что N делится на 16 и на x с остатком 4. Ясно, что x > 4.
N = 16x + 4
А когда он разложил те же N рыб по (x-1) рыбы, то у него все пакеты были заполнены.
Значит, N делится на (x-1) нацело, и получается неизвестное число пакетов.
Представим, что мы уже разложили по x рыб в 16 пакетов,
и 4 остались лишние.
Вынем из каждого пакета по 1 рыбе. Получится 16 пакетов по (x-1) рыбе и
16 + 4 = 20 рыб остается.
Значит, эти 20 рыб делятся на (x-1).
20 = 2*2*5 и имеет делители 1, 2, 4, 5, 10, 20.
x - 1 = 4, x = 5, N = 5*16 + 4 = 84 = 4*21
x - 1 = 5, x = 6, N = 6*16 + 4 = 100 = 5*20
x - 1 = 10, x = 11, N = 11*16 + 4 = 180 = 10*18
x - 1 = 20, x = 21, N = 21*16 + 4 = 340 = 20*17
1)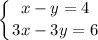
Система решений не имеет, так как отношения коэффициентов при переменных равны, но не равны отношению свободных членов.
--------------------------------------------------------------
2)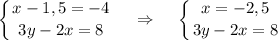
3y = 8 + 2·(-2,5); 3y = 3; y = 1
Система имеет единственное решение ( -2,5; 1)
Если предположить, что в условии опечатка : в первом уравнении потеряна переменная y, тогда система имеет вид
В таком виде система имеет бесконечно много решений, так как отношения коэффициентов при переменных равны отношению свободных членов.
Решения системы можно записать в виде (1,5y-4; y)
--------------------------------------------------------------
3)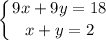
Система имеет бесконечно много решений, так как отношения коэффициентов при переменных равны отношению свободных членов.
Решения системы можно записать в виде (x; 2-x)