1. Сложение векторов AB + BC определяется из правила параллелограмма.
Путем параллельного переноса соединить начала обоих векторов в одной точке, достроить до параллелограмма. Диагональ параллелограмма является суммой двух векторов
Диагонали в точке пересечения M делятся пополам, т.е.
2) Длину вектора ВС можно найти по теореме Пифагора из прямоугольного треугольника ABM, в нем |BM|=|BD|/2 = 8 см; |AM| = 6 см
см
3) Для начала найдем координаты вектора АС:
2. 1) Координаты вектора АС:
Длина вектора АС: см
2) Координаты вектора BD:
Длина вектора BD: см
3.CT || AM || BP как перпендикулярны к одной прямой, значит четырехугольник AMTC - прямоугольная трапеция, BP - средняя линия трапеции, следовательно
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса: Не имеют корней; Имеют ровно один корень; Имеют два различных корня. В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.ДискриминантПусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно: Если D < 0, корней нет; Если D = 0, есть ровно один корень; Если D > 0, корней будет два.
1. Сложение векторов AB + BC определяется из правила параллелограмма.
Путем параллельного переноса соединить начала обоих векторов в одной точке, достроить до параллелограмма. Диагональ параллелограмма является суммой двух векторов
Диагонали в точке пересечения M делятся пополам, т.е.
2) Длину вектора ВС можно найти по теореме Пифагора из прямоугольного треугольника ABM, в нем |BM|=|BD|/2 = 8 см; |AM| = 6 см
3) Для начала найдем координаты вектора АС:
2. 1) Координаты вектора АС: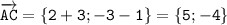
Длина вектора АС: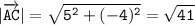 см
см
2) Координаты вектора BD: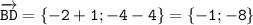
Длина вектора BD: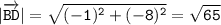 см
см
3.CT || AM || BP как перпендикулярны к одной прямой, значит четырехугольник AMTC - прямоугольная трапеция, BP - средняя линия трапеции, следовательно