Цен на продукты представляет собой ряд 3,4; 6,5; 2,8; 3,7; 5,1; 4,1; 5,9 процентов. найдите разницу между медианой и средним арифметическим этого ряда чисел
Возьмем за x- скорость 2 туриста. Тогда скорость первого будет x+2. Напишем время, за которое они добрались. время первого 40/(х+2) время второго 40/х Из условия ясно, что первый доехал быстрее, чем второй, значит мы можем записать уравнение:
- = 1 приводим к общему знаменателю:
= 1 Заметим, что x не равен 0, икс не равен -2. По свойству пропорций мы приходим к такому уравнению: 80=x^2+2x x^2+2x-80=0 По формуле четного корня находим дискриминант: D=p^2-ac=1+80=81; Корень из D=9 x1=-1-9=-10 (скорость не может быть отрицательной, поэтому посторонний корень) x2=-1+9=8 Итак, скорость второго туриста 8+2=10. ответ: скорость первого туриста 10 км/ч; скорость второго туриста 8км/ч
По клеточкам можно определить: из прямоугольного равнобедренного треугольника его углы будут равны 45°, 45° и 90°.
Так как угол развёрнутый, то угол наклона будет равен 180° - 45° = 135°.
Следовательно Тут коэффициент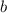 показывает пересечение графика функции с осью ординат
показывает пересечение графика функции с осью ординат 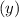 .
.
Из графика он равен 2.
Возьмём любую удобную точку из графика (кроме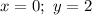 ):
):
Подставим их в формулу функции и получим:
ответ: -1.
Напишем время, за которое они добрались.
время первого 40/(х+2)
время второго 40/х
Из условия ясно, что первый доехал быстрее, чем второй, значит мы можем записать уравнение:
приводим к общему знаменателю:
Заметим, что x не равен 0, икс не равен -2.
По свойству пропорций мы приходим к такому уравнению:
80=x^2+2x
x^2+2x-80=0
По формуле четного корня находим дискриминант:
D=p^2-ac=1+80=81; Корень из D=9
x1=-1-9=-10 (скорость не может быть отрицательной, поэтому посторонний корень)
x2=-1+9=8
Итак, скорость второго туриста 8+2=10.
ответ: скорость первого туриста 10 км/ч; скорость второго туриста 8км/ч