Центростремительное ускорение при движении по окружности (в м/с2) можно
вычислить по формуле a = ω2R, где ω — угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 7,5 с−1, а центростремительное ускорение равно 337,5 м/с2.

Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.

1-ое свойство, которое понадобится

То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.

2-ое свойство, которое нам понадобится:

То есть довольно аналогичная вещь в произведении

На нашем примере все увидим

Находим остатки по модулю 31

Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,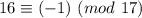 , но сейчас это не нужно), нам повезло, это 32

Учитываем, что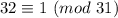 , получаем

То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым

Остаток 21, чудесно. Выполняем последний шаг.

То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.

У нас в итоге будет два числа: неизвестное (которое или которые станет/станут известным/и) и второе – разность изначально неизвестного и известного которая должна выражать дату (в каком-то неизвестном представлении).

Обозначим второе число (дата), как
тогда неизвестное число должно выглядеть, как:
и должно выполняться равенство:
или, иначе говоря: ;

Запишем это в столбик:



Все цифровые разряды будем, как это и принято, нумеровать от нуля до пяти, тогда номер разряда будет соответствовать индексу искомой цифры в разностном числе. Из столбика видно, что:



где: – возможная добавочная единица, уходящая из первого
и приходящая во второй разряд:

– возможная добавочная единица, уходящая из второго
и приходящая в третий разряд:

– возможная добавочная единица,
уходящая из третьего разряда в четвёртый:

После сложения уравнений системы, получаем:

;

Это возможно, только если и при ;

Отсюда следует, что: оба средних разряда при суммировании должны получать из предыдущего разряда добавочную единицу, причём второй разряд должен переполняться и иметь вычет десятки, а третий НЕ должен переполняться и не иметь вычета.

Тогда получим 6 возможных вариантов разностного числа:


Пятый разряд неизвестного числа должен быть больше пятого разряда разностного числа (верхней даты), а это значит, что нулевой разряд разного числа (верхней даты) должен быть больше неизвестного, стало быть, нулевой разряд при суммировании переполняется и даёт дополнительную единицу в первый разряд, а поскольку так как с этой цифры начинается разностное число.

Для того, чтобы второй разряд получал добавочную единицу, нужно чтобы первый разряд при суммировании переполнялся, что возможно только когда поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.

Значит, две последних цифры разностного числа (верхней даты) могут быть только годом, поскольку .

Стало быть, дни месяца и месяц
расположены в разрядах: .

Тогда остаётся три варианта разностного числа:



отсюда:



------------------

Рассмотрим первый вариант:
здесь может играть роль апреля.

Сказано, что сумма всех цифр должна быть кратна трём, тогда:



;

Возможны только случаи:

;

;

;

;

;

Учитывая, что:



получаем разностные числа:

– дата 12/04/56 г.
– дата 15/04/86 г.
– дата 21/04/47 г.
– дата 24/04/77 г.
– дата 24/04/38 г.

------------------

Рассмотрим второй вариант:
здесь может играть только роль числа месяца (дня).

Сказано, что сумма всех цифр должна быть кратна трём, тогда:



;

;

Возможен только один случай:

;

Учитывая, что:



получаем разностное число:

– дата 11/15/46 г.

продолжение >>>