Решение. Каждое из уравнений системы является линейным уравнением с двумя неизвестными. Нам известно, что графиком такого уравнения является прямая. Построим графики этих уравнений в одной системе координат.
Как мы видим, графики этих прямых пересекаются в точке с координатами . Что дает нам этот факт? Дело в том, что если точка принадлежит графику уравнения, то ее координаты удовлетворяют этому уравнению, то есть обращают его в верное числовое равенство. Так как точка пересечения одновременно принадлежит двум графикам уравнений, то ее координаты удовлетворяют одновременно обоим уравнениям, то есть координаты этой точки являются решением системы уравнений.
Мы использовали так называемый графический решения системы уравнений.
1)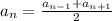
по формуле у нас все совпдает просто подставляем значения
x=0
2) формула n-го члена для последовательности первых членов 3,5,7,9
формула для n-члена выглядит так:
a1 это первый член
n это номер какого то члена (например 17-ый ; 20-ый)
d это разность то есть на какое число отличается какойто член от предыдущего
у нас известен первый член и несколько последующих
нам нужно только найти d вычтем от друг друга два последовательных члена к примеру 7 и 9 получается 2
значит d=2
Объяснение:
Решение. Каждое из уравнений системы является линейным уравнением с двумя неизвестными. Нам известно, что графиком такого уравнения является прямая. Построим графики этих уравнений в одной системе координат.
Как мы видим, графики этих прямых пересекаются в точке с координатами . Что дает нам этот факт? Дело в том, что если точка принадлежит графику уравнения, то ее координаты удовлетворяют этому уравнению, то есть обращают его в верное числовое равенство. Так как точка пересечения одновременно принадлежит двум графикам уравнений, то ее координаты удовлетворяют одновременно обоим уравнениям, то есть координаты этой точки являются решением системы уравнений.
Мы использовали так называемый графический решения системы уравнений.