Войти Регистрация Спроси ai-bota

Цифрларының айырмасы 2- ге тең, ал олардың квадраттарының
қосындысы52 ге тең болатын екі
таібалы сан болатынын зерттеңдер.

Показать ответ

Ответ:

Сабина11123

27.12.2021 12:32

Белыми струйками сыпался с деревьев снег. Кое-где на снег с легким стуком падали тяжелые весенние капли. Весна! В это утро она впервые заявила о себе так решительно и настойчиво.

Словосочетания: белыми струйками, легким стуком, тяжелые капли, весенние капли.

Морфологический анализ прилагательных.

Белыми - имя прилагательное, обозначает признак предмета, вопрос: какими?

начальная форма - белый

постоянные признаки: качественное;

непостоянные признаки: полное, множественное число, творительный падеж;

в предложении - определение.

Легким - имя прилагательное, обозначает признак предмета, вопрос: каким?

начальная форма - легкий

постоянные признаки: качественное;

непостоянные признаки: полное, единственное число, творительный падеж;

в предложении - определение.

Тяжелые - имя прилагательное, обозначает признак предмета, вопрос: какие?

начальная форма - тяжелый

постоянные признаки: качественное;

непостоянные признаки: полное, множественное число, именительный падеж;

в предложении - определение.

Весенние - имя прилагательное, обозначает признак предмета, вопрос: какие?

начальная форма - весенний

постоянные признаки: относительное;

непостоянные признаки: множественное число, именительный падеж;

в предложении - определение.

0,0(0 оценок)

Ответ:

лололололлоло97

28.10.2020 09:53

Дана система уравнений:

$\begin{cases} x^{2}-2y^{2}=17,\\x^{2}-2xy=-3.\end{cases}$

Из второго уравнения системы выразим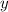 через , получим:

$y=\frac{x^{2}+3}{2x}$ --------(1)

Поскольку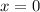 x=0 не является корнем 2-го уравнения нашей системы, то подставив в первое уравнения системы вместо 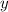выражение (1), мы не потеряем решений системы:

$x^{2}-2*\frac{(x^{2}+3)^{2}}{(2x)^{2}}=17$ , отсюда

$\frac{2x^{4}-x^{4}-6x^{2}-9}{2x^{2}}=17$ , отсюда

$x^{4}-40x^{2}-9=0$ ---------(2)

Замена: пусть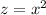 $z=x^{2}$ , тогда (2) примет вид:

$z^{2}-40z-9=0$ --------(3)

(3) - квадратное уравнение относительно

D=1600+4*9=1636

$z_{1}=\frac{40+2*\sqrt{409}}{2}=20+\sqrt{409}$

$z_{2}=\frac{40-2*\sqrt{409}}{2}=20-\sqrt{409}<0$

Но второй корень не удовлетворяет условию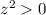 $z^{2}0$

Возвращаясь к старой неизвестной, получим:

$x^{2}=z_{1}=\frac{40+2*\sqrt{409}}{2}=20+\sqrt{409}$ -------(4)

Из (4) получаем два значения :

$x_{1}=\sqrt{20+\sqrt{409}}$

$x_{1}=-\sqrt{20+\sqrt{409}}$

Подставим в первое уравнение системы вместо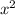 $x^{2}$ выражение (4), найдем соответствующие значения :

$20+\sqrt{409}-2y^{2}=17$ , отсюда

$y^{2}=\frac{3+\sqrt{409}}{2}$ --------(5)

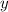Из (5) получаем два значения :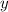

$y_{1}=\sqrt{\frac{3+\sqrt{409}}{2}}$

$y_{2}=-\sqrt{\frac{3+\sqrt{409}}{2}}$

Итак, наша система имеет четыре решения:

$(\sqrt{20+\sqrt{409}}; \sqrt{\frac{3+\sqrt{409}}{2}})$

$(\sqrt{20+\sqrt{409}}; -\sqrt{\frac{3+\sqrt{409}}{2}})$

$(-\sqrt{20+\sqrt{409}}; \sqrt{\frac{3+\sqrt{409}}{2}})$

$(-\sqrt{20+\sqrt{409}}; -\sqrt{\frac{3+\sqrt{409}}{2}})$

0,0(0 оценок)

Популярные вопросы: Алгебра

кристина1423

22.07.2022 11:38

Решить sin^2 π/8 + cos^2 π/8 - √2 sin t = 0...

неманема

22.07.2022 11:38

Сравните значения выражения 0.2y-3и0.3y-4 при y=6...

mashA2007111

22.07.2022 11:38

Определите имеет ли смысл выражение 1.arcsin(x-1) при x=корень5; x=0,9; x=sin(-пи/6) 2.arccos(x+1) при x= - корень 3; x=cosпи/3; x=-1/3. подробно...

cawa1303

26.01.2020 13:52

1) lg(x-0.09)+log_0.01(9)=0 2) log_0.25(6x-5)=-2...

karpovkonstanti

27.02.2021 06:45

Представьте данное число в виде степени какого-либо числа с показателем, отличным от 1 а) 128; б) 27; в) 25 / 49 г) 10 000 07.12.2012...

zaira1979zaira11

23.01.2021 04:21

№1. число b кратно 7. докажите, что 6b кратно 42.№ 2. число n кратно 6. докажите, что (n^2+8n) кратно 16. № 3. числа p и q таковы, что p кратно 5, q кратно 8. докажите,...

maria3317

17.11.2021 06:42

Складіть квадратне рівняння, у якого: старший коефіцієнт дорівнює ⅚, другий коефіцієнт дорівнює -2, а вільний член дорівнює 0....

Den5220

17.11.2021 06:42

Виразіть із рівняння 3х-у= -5 змінну х через змінну у...

anjutaboyycova

10.01.2021 01:36

Знайдіть неповний квадрат суми виразів 4 i y(квадрат)...

Алиса228228

20.10.2022 16:13

Найти b₁ геометрической прогрессии (bₙ) и номер n, если:bₙ=432Sₙ=624q=3...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку