Умножим на :
Разделим каждый член на и упростим.
Перепишем уравнение с абсолютным значением без знака модуля:
После упрощения остаются только два уникальных уравнения, которые нам предстоит решить:
Решим относительно x:
Запишем все решения:
Умножим на
на 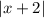 :
:
Разделим каждый член на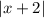 и упростим.
и упростим.
Перепишем уравнение с абсолютным значением без знака модуля:
После упрощения остаются только два уникальных уравнения, которые нам предстоит решить:
Решим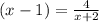 относительно x:
относительно x:
Решим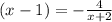 относительно x:
относительно x:
Запишем все решения:
(х-1)*(х+2)=4
(х+1)*(х+2)=-4
х=2
х=-3
х=-3,х=2