Воспользуемся формулой разности косинусов:
Имеем:
Поделим обе части на :
Воспользуемся формулой: , n ∈ Z
, n ∈ Z
Воспользуемся формулой разности косинусов:
Имеем:
Поделим обе части на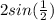 :
:
Воспользуемся формулой: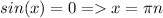 , n ∈ Z
, n ∈ Z