Дам 40б а) Велосипедист решил совершить путешествие, потратив на дорогу 11 часов. Длина всего маршрута равна 180 км. На второй половине пути скорость велосипедиста была на 3 км/ч меньше, чем его скорость на первой половине пути. Определите, с какой скоростью двигался велосипедист на первой половине пути

Показать ответ

Ответ:

vkunney

24.09.2021 01:41

Чтобы уравнение имело действительное решение , достаточно чтобы дискриминант был неотрицательным.

D/4 = (a^3-b^3)^2 -(a^2-b^2)*(a^4-b^4)>=0

То есть , необходимо доказать , что при любых a и b справедливо строгое неравенство :

(a^3-b^3)^2>=(a^2-b^2)*(a^4-b^4)

(a-b)^2*(a^2+ab+b^2)^2>=(a-b)^2* (a+b)^2 * (a^2+b^2)

Заметим , что когда a=b , получаем что 0=0 , то есть условие выполнено. И в этом случае уравнение имеет бесконечно много решений.

Теперь, поскольку мы разобрали этот случай и (a-b)^2>=0 , то для случая a≠b , можно поделить обе части неравентсва на (a-b)^2 не меняя знак неравенства :

(a^2+ab+b^2)^2>=(a+b)^2*(a^2+b^2)

( a^2+ab+b^2)^2 >= (a^2+2ab+b^2)*(a^2+b^2)

Теперь сделаем слудующий прием , поскольку (a^2+b^2)^2>0 при a≠b≠0

То можно поделить на это выражение обе части неравенства не меняя его знак :

( 1+ ab/(a^2+b^2) )^2>= 1+ 2ab/(a^2+b^2)

Тогда можно сделать замену:

ab/(a^2+b^2)=t

(1+t)^2>=1+2t

t^2+2t+1>=1+2t

t^2>=0 (верно)

Таким образом :

(a^3-b^3)^2>=(a^2-b^2)*(a^4-b^4) , то есть D>=0.

Вывод : уравнение имеет действительное решение при любых действительных а и b.

Что и требовалось доказать.

0,0(0 оценок)

Ответ:

Boxing12474

26.06.2021 02:26

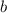Пусть прямоугольник содержит строк и столбцов. Найдем его площадь:

S=ab

По смыслу задачи это искомое число клеток прямоугольника. Обозначим его буквой М, где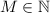 $M\in\mathbb{N}$ :

M=ab

Закрашенные ячейки содержат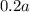 0.2a строк и 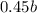0.45b столбцов. Найдем площадь закрашенной области:

$S_0=0.2a\cdot0.45b=0.09ab$

S_0=0.09M

Но закрашенная область - это квадрат. Найдем его сторону:

$a_0=\sqrt{S_0} =\sqrt{0.09M}=0.3\sqrt{M}$

Полученное число соответствует некоторому количеству клеток, а значит должно быть натуральным:

$0.3\sqrt{M}\in\mathbb{N}$

Кроме этого, число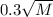 $0.3\sqrt{M}$ составляет 20 % и 45 % от натуральных чисел, выражающих количество строк и столбцов в исходном прямоугольнике. то есть:

$\left(0.3\sqrt{M}:0.2\right)\in\mathbb{N}$

$\left(0.3\sqrt{M}:0.45\right)\in\mathbb{N}$

Преобразуем числа:

$0.3\sqrt{M}:0.2=0.3\sqrt{M}:\dfrac{1}{5} =5\cdot0.3\sqrt{M}$

$0.3\sqrt{M}:0.45=\dfrac{3}{10} \sqrt{M}:\dfrac{9}{20} =\dfrac{3}{10} \cdot\dfrac{20}{9}\sqrt{M}=\dfrac{2}{3}\sqrt{M}$

Заметим, что первое условие выполняется при ранее поставленном условии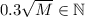 $0.3\sqrt{M}\in\mathbb{N}$ , поэтому его далее учитывать не будем.

Таким образом должно выполниться два условия:

$\begin{cases} 0.3\sqrt{M}\in\mathbb{N} \\ \dfrac{2}{3}\sqrt{M}\in\mathbb{N}\end{cases}$

Эти условия можно объединить в одно.

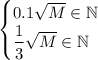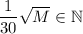Если выполнятся условия $\begin{cases} 0.1\sqrt{M}\in\mathbb{N} \\ \dfrac{1}{3}\sqrt{M}\in\mathbb{N}\end{cases}$ , то и предыдущие условия будут верны. А для проверки этих условий достаточно проверить, что $\dfrac{1}{30}\sqrt{M}\in\mathbb{N}$ .