Дан график движения группы туристов, отправляющихся с турбазы в город. Сначала Туристы шли по проселочной дороге до остановки автобуса, А оставшуюся часть пути проехали на автобусе. Пользуясь графиком, ответь на вопросы;
A)Сколько времени туристы шли по проселочной дороге;
Б)Сколько времени ждали туристы ждали автобус;
В)С какой скоростью они шли по проселочной дороге?

Показать ответ

Ответ:

гнеуй

29.12.2020 21:28

1) S(полной поверхности) = S(боковой поверхности) + 2S(основания) = 12 + 72 = 84 кв.см

2)т.к. в основании прямоугольный треугольник, то его площадь расчитывается как половина произведения катетов: 2S(основания) = 2*(1/2 * 3* 4 ) = 12 квадратным сантиметрам.

3) по теореме: S(боковой поверхности) = произведению периметра основания на высоту призмы, имеем: 6Роснования.

Гиппотенузу основания находим по теореме пифагора, получаем 5см. Тогда Р основания = 5+4+3 = 12 см. А S(боковой поверхности) = 6*12 = 72 кв.см.

0,0(0 оценок)

Ответ:

луя3

16.08.2022 01:35

Объяснение:

y=-x^2+6x-10 , $D(y)=[3;+\infty)$

данная функция квадратическая, ее график парабола состоит из двух ветвей с общей точкой - вершиной параболы, которые в общем случае делят ее на две подфункции, у каждой из которых своя своя обратная функция

так в базовом виде это для параболы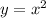 y=x^2 вершина (0;0) можно выделить две обратные функц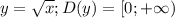ии $y=\sqrt{x}; D(y)= [0;+\infty)$ и $y=\sqrt{-x}; D(y)=(-\infty; 0]$

для данной параболы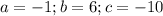 a=-1;b=6;c=-10

$x_W=-\frac{b}{2a}=-\frac{6}{2*(-1)}=3$

$y_W=c-\frac{b^2}{4a}=-10-\frac{6^2}{4*(-1)}=-10+9=-1$

а значит имеем одну ветвь параболы

$D(y)=[3;+\infty); a$

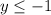( $y \leq -1$ )

y=-x^2+6x-10=-x^2+6x-9-1=-(x^2-6x+9)-1=-(x^2-2*x*3+3^2)-1

y=-(x-3)^2-1

y+1=-(x-3)^2;-y-1=(x-3)^2

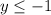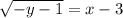
так как $y \leq -1$ : $\sqrt{-y-1}=x-3$

$x(y)=3+\sqrt{-y-1}$ --- график тот же что и у исходной функции, но "обратная" зависимость переменных

меняем обозначения (x,y)->(y,x) и получим что

$y(x)=3+\sqrt{-x-1}$ , $D(y)=[-\infty; -1]$ А это уравнение обратной функции, график симметричен исходной функции относительно прямой y=x

------------------------------------------------------------------------------------

$y(x)=f(x)=-x^2+6x-10, D(y)=[3;+\infty)$

$y(x)=f^{-1} (x)=3+\sqrt{-x-1}, D(y)=[-\infty; -1]$

$f^{-1}(f(x))=x, x \geq 3$

$(3+\sqrt{-(-x^2+6x-10)-1}=3+\sqrt{x^2-6x+10-1}=3+\sqrt{x^2-6x+9}=$

$=3+\sqrt{(x-3)^2}=3+|x-3|=|| x \geq 3 || =3+x-3=x$

аналогично можно убедиться (помним только про области определения и действий функций), что

$f(f^{-1}x)=x; -(3+\sqrt{-x-1})^2+6(3+\sqrt{-x-1})-10=x, x \leq -1$

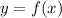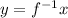!! следует понимать что по факту есть две функции y=f(x) и $y=f^{-1}x$ , x всего лишь условная буква, обозначающая независимый аргумент, y - условная буква, обозначающая значение функции - на их месте могли быть и другие буквы,

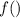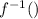более важную роль для понимания обратных функций играет сами f() и $f^{-1} ()$ . (соблюдение взаимно однозначности), а х и y лишь для работы в системе координат XoY