Дан квадратный трехчлен , все коэффициенты которого отличны от нуля. если поменять местами коэффициенты a и b, то трехчлен будет иметь один корень. если поменять местами b и c, то трехчлен также имеет один корень. найдите, сколько корней имеет трехчлен . (ответ без решения не засчитываю! )
из условия задачи: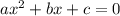
решим систему уравнений, где в одном поменяем a и b, а в другом b и c.
выразим дискриминант в обоих уравнениях и приравняем к 0, т.к. корень должен быть 1.
выразим 4b из первого уравнения и подставим во второе:
т.к.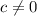
тогда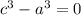
подставим в выражение, где твыразили 4b
подставим все получившиеся коэффициенты в первое уравнеие:
выразим дискриминант:
видно, что дискриминант получится отрицательным, следовательно у данного трехчлена решений нет.
ответ: корней нет