Дана алгебраическая дробь m−3/m−12.

1) При каких значениях переменной значение дроби равно нулю?
Если m=
.

2) При каких значениях переменной дробь не определена?
Если m=

Показать ответ

Ответ:

kaskovam

17.02.2020 01:54

Відповідь:

Пояснення:

Нехай перше та друге числа — x та y відповідно. Отже, числа x, y і 12 утворюють геометричну прогресію, а числа x, y і -36 — арифметичну.

Скористаємося основними властивостями цих прогресій. Квадрат кожного члена геометричної дорівнює добутку сусідніх. Зокрема для члена y,

$y^2=12x \; (*)$

Кожен член арифметичної прогресії дорівнює середньому арифметичному сусідніх. Зокрема для того ж члена y,

$y=\frac{x-36}{2}$ .

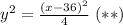Звідси $y^2=\frac{(x-36)^2}{4} \; (**)$ .

Ліві частини рівнянь (*) і (**) збігаються, тому прирівняємо праві та знайдемо x:

$12x=\frac{(x-36)^2}{4}\\48x=(x-36)^2\\48x=x^2-72x+1296\\x^2-120x+1296=0\\D_1=k^2-ac=(-60)^2-1296=3600-1296=2304\\x=\frac{-k\pm \sqrt{D_1}}{a}\\\begin{cases} x_1=\frac{60+\sqrt{2304} }{1}=60+48=108\\x_2=\frac{60-\sqrt{2304} }{1}=60-48=12 \end{cases}$

Якщо перше з розглядуваних чисел — 12, то друге дорівнює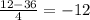 $\frac{12-36}{4}=-12$ . Воно не натуральне й не задовольняє умові. Якщо ж x=108, то 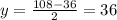$y=\frac{108-36}{2}=36$ , що цілком відповідає умові задачі.

Тоді сума цифр першого числа 1+0+8=9.

0,0(0 оценок)

Ответ:

kwasmarianna

12.06.2021 23:31

Средняя скорость первого туриста:

r/2 + √((r²/4) +sr/4n);

Средняя скорость второго туриста:

- (r/2 - √((r²/4) +sr/4n))

Объяснение:

Пусть х и у - скорости движения первого и второго туристов, а t - время их движения, если бы они шли с одинаковой скоростью, тогда:

s/x = t-n - фактическое время движение первого туриста, (1)

s/y = t+3n - фактическое время движения второго туриста. (2)

Из второго уравнения вычтем первое:

s/y - s/x = t+3n - (t-n)

s/y - s/x = t+3n - t+n

s(1/y - 1/x) = 4n

s[(х-у)/ху] = 4n (3)

так как (х-у) = r (согласно условию), (4)

то подставим (4) в (3):

sr/ху = 4n

ху = sr/4n (5).

Согласно теореме Виета, сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а их произведение равно свободному члену.

Обозначим переменную v.

Тогда приведённое квадратное уравнение c учетом (4) и (5) имеет вид:

v² - rv - sr/4n = 0, (6)

так как

х + (-у) = r

х· (-у) = - sr/4n.

Соответственно скорости равны:

v₁ = х = r/2 + √((r²/4) +sr/4n)

v₂ = - y = - (r/2 - √((r²/4) +sr/4n))

ответ: средняя скорость первого туриста:

r/2 + √((r²/4) +sr/4n);

средняя скорость второго туриста: